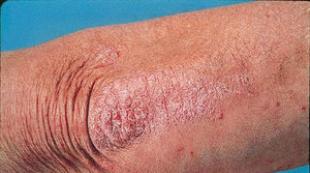
Kako su povezane determinante izravne i inverzne matrice? Matrična metoda za rješavanje slougha: primjer rješenja pomoću inverzne matrice

Algebra matrica - Inverzna matrica

inverzna matrica

Inverzna matrica je matrica koja, kada se pomnoži i desno i lijevo danom matricom, daje matricu identiteta.
Označimo inverznu matricu matrice A kroz , tada prema definiciji dobivamo:

Gdje E- Matrica identiteta.
Kvadratna matrica nazvao nije posebno (nedegeneriran) ako njegova determinanta nije nula. Inače se zove poseban (degenerirati) ili jednina.

Teorem vrijedi: Svaka nesingularna matrica ima inverznu matricu.

Operacija pronalaženja inverzne matrice se zove apel matrice. Razmotrimo algoritam inverzije matrice. Neka je dana nesingularna matrica n-ti red:

gdje je Δ = det A ≠ 0.

Algebarsko zbrajanje elementa matrice n-ti red A naziva se determinanta matrice uzeta s određenim predznakom ( n–1) red dobiven brisanjem ja-th line i j stupac matrice A:

Stvorimo tzv u prilogu matrica:

gdje su algebarski komplementi odgovarajućih elemenata matrice A.
Imajte na umu da algebarsko sabiranje elemenata retka matrice A nalaze se u odgovarajućim stupcima matrice à , odnosno matrica se transponira u isto vrijeme.
Dijeljenjem svih elemenata matrice à po Δ – vrijednost determinante matrice A, kao rezultat dobivamo inverznu matricu:

Zabilježimo niz posebnih svojstava inverzne matrice:
1) za zadanu matricu A svoju inverznu matricu je jedini;
2) ako postoji inverzna matrica, tada desno obrnuto I lijevi revers matrice se podudaraju s njim;
3) singularna (singularna) kvadratna matrica nema inverznu matricu.

Osnovna svojstva inverzne matrice:
1) determinanta inverzne matrice i determinanta izvorne matrice su recipročne vrijednosti;
2) inverzna matrica proizvoda kvadratnih matrica jednaka je proizvodu inverzne matrice faktora, uzetih obrnutim redoslijedom:

3) transponirana inverzna matrica jednaka je inverznoj matrici dane transponirane matrice:

PRIMJER Izračunajte inverz zadane matrice.

1. Odredite determinantu izvorne matrice. Ako je , tada je matrica singularna i ne postoji inverzna matrica. Ako, tada postoji nedegenerirana i inverzna matrica.

2. Pronađite matricu transponiranu na.

3. Naći algebarske komplemente elemenata i od njih sastaviti adjungiranu matricu.

4. Inverznu matricu sastavljamo pomoću formule.

5. Provjeravamo ispravnost izračuna inverzne matrice, na temelju njene definicije:.

Primjer. Nađite matricu inverznu ovoj: .

Riješenje.

1) Matrična determinanta

.

2) Naći algebarske komplemente elemenata matrice i od njih sastaviti adjungiranu matricu:

3) Izračunajte inverznu matricu:

,

4) Provjerite:

№4Rang matrice. Linearna neovisnost redaka matrice

Za rješavanje i proučavanje brojnih matematičkih i primijenjenih problema važan je koncept ranga matrice.

U matrici veličine, brisanjem svih redaka i stupaca, možete izolirati kvadratne podmatrice th reda, gdje. Determinante takvih podmatrica nazivaju se minori matričnog reda .

Na primjer, iz matrica možete dobiti podmatrice 1., 2. i 3. reda.

Definicija. Rang matrice je najviši red minora različitih od nule te matrice. Oznaka: ili.

Iz definicije slijedi:

1) Rang matrice ne prelazi manju od njezinih dimenzija, tj.

2) ako i samo ako su svi elementi matrice jednaki nuli, tj.

3) Za kvadratnu matricu n-tog reda ako i samo ako je matrica nesingularna.

Budući da je izravno nabrajanje svih mogućih minora matrice, počevši od najveće veličine, teško (oduzima puno vremena), koriste se elementarne transformacije matrice koje čuvaju rang matrice.

Elementarne transformacije matrica:

1) Odbacivanje nultog retka (stupca).

2) Množenje svih elemenata retka (stupca) brojem.

3) Promjena redoslijeda redaka (kolona) matrice.

4) Dodavanje svakom elementu jednog retka (stupca) odgovarajućih elemenata drugog retka (stupca), pomnoženih bilo kojim brojem.

5) Transpozicija matrice.

Definicija. Matrica dobivena iz matrice pomoću elementarnih transformacija naziva se ekvivalentna i označava A U.

Teorema. Rang matrice se ne mijenja tijekom elementarnih transformacija matrice.

Pomoću elementarnih transformacija matricu možete svesti na takozvani stepenasti oblik, pri čemu izračunavanje njezinog ranga nije teško.

Matrica se naziva ešalon ako ima oblik:

Očigledno, rang matrice koraka je jednak broju redaka koji nisu nula, jer postoji manji poredak koji nije jednak nuli:

.

Primjer. Odrediti rang matrice pomoću elementarnih transformacija.

Rang matrice je jednak broju redova koji nisu nula, tj. .

№5Linearna neovisnost redaka matrice

S obzirom na matricu veličina

Označimo redove matrice na sljedeći način:

Dvije linije se nazivaju jednak , ako su im odgovarajući elementi jednaki. .

Uvedimo operacije množenja niza brojem i zbrajanja nizova kao operacije koje se izvode element po element:

Definicija. Red se naziva linearnom kombinacijom redaka matrice ako je jednak zbroju umnožaka tih redaka s proizvoljnim realnim brojevima (bilo kojim brojevima):

Definicija. Redovi matrice se nazivaju linearno ovisna , ako postoje brojevi koji nisu istovremeno jednaki nuli, tako da je linearna kombinacija redaka matrice jednaka nultom redu:

Gdje . (1.1)

Linearna ovisnost redaka matrice znači da je barem 1 redak matrice linearna kombinacija ostatka.

Definicija. Ako je linearna kombinacija redaka (1.1) jednaka nuli ako i samo ako su svi koeficijenti , tada se redovi nazivaju linearno neovisni .

Teorem o rangu matrice . Rang matrice jednak je maksimalnom broju njenih linearno nezavisnih redaka ili stupaca kroz koje se linearno izražavaju svi ostali redovi (stupci).

Teorem igra temeljnu ulogu u matričnoj analizi, posebno u proučavanju sustava linearnih jednadžbi.

№6Rješavanje sustava linearnih jednadžbi s nepoznanicama

Sustavi linearnih jednadžbi naširoko se koriste u ekonomiji.

Sustav linearnih jednadžbi s varijablama ima oblik:

,

gdje su () proizvoljni pozvani brojevi koeficijenti za varijable I slobodni članovi jednadžbi , odnosno.

Kratak zapis: ().

Definicija. Rješenje sustava je takav skup vrijednosti, čijom se zamjenom svaka jednadžba sustava pretvara u pravu jednakost.

1) Sustav jednadžbi naziva se spojnica , ako ima barem jedno rješenje, i nezglobni, ako nema rješenja.

2) Simultani sustav jednadžbi naziva se određeni , ako ima jedinstveno rješenje, i neizvjestan , ako ima više od jednog rješenja.

3) Dva sustava jednadžbi nazivaju se ekvivalent (ekvivalent ) , ako imaju isti skup rješenja (na primjer, jedno rješenje).

Ova tema jedna je od najomraženijih među studentima. Gore su, vjerojatno, kvalifikacije.

Trik je u tome što nas sam koncept inverznog elementa (ne govorim samo o matricama) upućuje na operaciju množenja. Čak iu školskom kurikulumu množenje se smatra složenom operacijom, a množenje matrica općenito je zasebna tema, kojoj sam posvetio cijeli paragraf i video lekciju.

Danas nećemo ulaziti u detalje matričnih izračuna. Prisjetimo se samo: kako se matrice označavaju, kako se množe i što iz toga slijedi.

Pregled: Množenje matrice

Prije svega, dogovorimo se oko notacije. Matrica $A$ veličine $\left[ m\times n \right]$ jednostavno je tablica brojeva s točno $m$ redaka i $n$ stupaca:

\=\underbrace(\left[ \begin(matrix) ((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) \\ (( a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) \\ ... & ... & ... & ... \\ ((a)_(m1)) & ((a)_(m2)) & ... & ((a)_(mn)) \\\end(matrica) \desno])_(n)\]

Da ne biste slučajno pomiješali retke i stupce (vjerujte mi, na ispitu možete pobrkati jedinicu s dvojkom, a kamoli neke retke), samo pogledajte sliku:

Određivanje indeksa za ćelije matrice

Što se događa? Ako postavite standardni koordinatni sustav $OXY$ u gornji lijevi kut i usmjerite osi tako da pokrivaju cijelu matricu, tada se svaka ćelija ove matrice može jedinstveno povezati s koordinatama $\left(x;y \right)$ - ovo će biti broj retka i broj stupca.

Zašto je koordinatni sustav smješten u gornjem lijevom kutu? Da, jer odatle počinjemo čitati sve tekstove. Vrlo je lako zapamtiti.

Zašto je $x$ os usmjerena prema dolje, a ne udesno? Opet, jednostavno je: uzmite standardni koordinatni sustav ($x$-os ide udesno, $y$-os ide gore) i zarotirajte ga tako da pokrije matricu. Ovo je rotacija od 90 stupnjeva u smjeru kazaljke na satu - rezultat vidimo na slici.

Općenito, shvatili smo kako odrediti indekse elemenata matrice. Sada pogledajmo množenje.

Definicija. Matrice $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$, kada se broj stupaca u prvoj podudara s brojem redaka u drugoj, su naziva dosljednim.

Upravo tim redom. Netko se može zbuniti i reći da matrice $A$ i $B$ tvore uređeni par $\left(A;B \right)$: ako su konzistentne u ovom redoslijedu, onda uopće nije nužno da $B $ i $A$ oni. par $\left(B;A \right)$ također je konzistentan.

Samo se uparene matrice mogu množiti.

Definicija. Umnožak usklađenih matrica $A=\left[ m\times n \right]$ i $B=\left[ n\times k \right]$ nova je matrica $C=\left[ m\times k \right ]$ , čiji se elementi $((c)_(ij))$ izračunavaju prema formuli:

\[((c)_(ij))=\sum\limits_(k=1)^(n)(((a)_(ik)))\cdot ((b)_(kj))\]

Drugim riječima: da biste dobili element $((c)_(ij))$ matrice $C=A\cdot B$, trebate uzeti $i$-redak prve matrice, $j$ -ti stupac druge matrice, a zatim pomnožite u parovima elemente iz tog retka i stupca. Zbrojite rezultate.

Da, to je tako surova definicija. Iz toga odmah proizlazi nekoliko činjenica:

1. Množenje matrica, općenito govoreći, nije komutativno: $A\cdot B\ne B\cdot A$;
2. Međutim, množenje je asocijativno: $\lijevo(A\cdot B \desno)\cdot C=A\cdot \lijevo(B\cdot C \desno)$;
3. Pa čak i distributivno: $\lijevo(A+B \desno)\cdot C=A\cdot C+B\cdot C$;
4. I još jednom distributivno: $A\cdot \lijevo(B+C \desno)=A\cdot B+A\cdot C$.

Distributivnost množenja je morala biti posebno opisana za lijevi i desni faktor zbroja upravo zbog nekomutativnosti operacije množenja.

Ako se pokaže da je $A\cdot B=B\cdot A$, takve se matrice nazivaju komutativnima.

Među svim matricama koje se tamo nečim množe, postoje posebne - one koje, kada se pomnože s bilo kojom matricom $A$, opet daju $A$:

Definicija. Matrica $E$ naziva se identitetom ako je $A\cdot E=A$ ili $E\cdot A=A$. U slučaju kvadratne matrice $A$ možemo napisati:

Matrica identiteta je čest gost pri rješavanju matričnih jednadžbi. I općenito, čest gost u svijetu matrica. :)

I zbog ovog $E$ netko je smislio sve one gluposti koje će biti sljedeće napisane.

Što je inverzna matrica

Budući da je množenje matrica vrlo radno intenzivna operacija (morate pomnožiti hrpu redaka i stupaca), koncept inverzne matrice također se nije pokazao najtrivijalnijim. I zahtijeva neko objašnjenje.

Ključna definicija

Pa, vrijeme je da saznamo istinu.

Definicija. Matrica $B$ naziva se inverzom matrice $A$ ako

Inverzna matrica je označena sa $((A)^(-1))$ (ne brkati sa stupnjem!), tako da se definicija može prepisati na sljedeći način:

Čini se da je sve vrlo jednostavno i jasno. Ali kada se analizira ova definicija, odmah se postavlja nekoliko pitanja:

1. Postoji li uvijek inverzna matrica? A ako ne uvijek, kako onda odrediti: kada postoji, a kada ne?
2. I tko je rekao da postoji točno jedna takva matrica? Što ako za neku početnu matricu $A$ postoji cijela gomila inverza?
3. Kako izgledaju svi ti "obrati"? I kako, točno, da ih brojimo?

Što se tiče algoritama izračuna, o tome ćemo govoriti malo kasnije. No, na preostala pitanja ćemo odgovoriti upravo sada. Formulirajmo ih u obliku zasebnih iskaza-lema.

Osnovna svojstva

Počnimo s tim kako bi matrica $A$ trebala izgledati u principu da bi za nju postojao $((A)^(-1))$. Sada ćemo provjeriti moraju li obje ove matrice biti kvadratne i iste veličine: $\left[ n\times n \right]$.

Lema 1. Dana je matrica $A$ i njezin inverz $((A)^(-1))$. Tada su obje ove matrice kvadratne i istog reda $n$.

Dokaz. Jednostavno je. Neka je matrica $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ a\times b \right]$. Budući da umnožak $A\cdot ((A)^(-1))=E$ postoji po definiciji, matrice $A$ i $((A)^(-1))$ su dosljedne prikazanim redoslijedom:

\[\begin(align) & \left[ m\times n \right]\cdot \left[ a\times b \right]=\left[ m\times b \right] \\ & n=a \end( uskladiti)\]

Ovo je izravna posljedica algoritma množenja matrice: koeficijenti $n$ i $a$ su "tranzitni" i moraju biti jednaki.

Ujedno je definirano i inverzno množenje: $((A)^(-1))\cdot A=E$, stoga su matrice $((A)^(-1))$ i $A$ također dosljedno navedenim redoslijedom:

\[\begin(align) & \left[ a\times b \right]\cdot \left[ m\times n \right]=\left[ a\times n \right] \\ & b=m \end( uskladiti)\]

Stoga, bez gubitka općenitosti, možemo pretpostaviti da je $A=\left[ m\times n \right]$, $((A)^(-1))=\left[ n\times m \right]$. Međutim, prema definiciji $A\cdot ((A)^(-1))=((A)^(-1))\cdot A$, stoga se veličine matrica strogo podudaraju:

\[\begin(align) & \left[ m\times n \right]=\left[ n\times m \right] \\ & m=n \end(align)\]

Dakle, ispada da su sve tri matrice - $A$, $((A)^(-1))$ i $E$ - kvadratne matrice veličine $\left[ n\times n \right]$. Lema je dokazana.

Pa to je već dobro. Vidimo da su samo kvadratne matrice invertibilne. Sada se uvjerimo da je inverzna matrica uvijek ista.

Lema 2. Dana je matrica $A$ i njezin inverz $((A)^(-1))$. Tada je ova inverzna matrica jedina.

Dokaz. Idemo kontradiktorno: neka matrica $A$ ima barem dva inverza - $B$ i $C$. Tada su prema definiciji istinite jednakosti:

\[\begin(align) & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end(align)\]

Iz leme 1 zaključujemo da su sve četiri matrice - $A$, $B$, $C$ i $E$ - kvadrati istog reda: $\left[ n\times n \right]$. Stoga je proizvod definiran:

Budući da je množenje matrica asocijativno (ali ne i komutativno!), možemo napisati:

\[\begin(align) & B\cdot A\cdot C=\lijevo(B\cdot A \desno)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \lijevo(A\cdot C \desno)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end(align)\]

Dobili smo jedinu moguću opciju: dvije kopije inverzne matrice su jednake. Lema je dokazana.

Gornji argumenti gotovo doslovce ponavljaju dokaz jedinstvenosti inverznog elementa za sve realne brojeve $b\ne 0$. Jedini značajan dodatak je uzimanje u obzir dimenzija matrica.

Međutim, još uvijek ne znamo ništa o tome je li svaka kvadratna matrica invertibilna. Ovdje nam u pomoć dolazi determinanta - to je ključna karakteristika za sve kvadratne matrice.

Lema 3. Zadana je matrica $A$. Ako njegova inverzna matrica $((A)^(-1))$ postoji, tada je determinanta izvorne matrice različita od nule:

\[\lijevo| A\desno|\ne 0\]

Dokaz. Već znamo da su $A$ i $((A)^(-1))$ kvadratne matrice veličine $\left[ n\times n \right]$. Stoga za svaku od njih možemo izračunati determinantu: $\left| A\desno|$ i $\lijevo| ((A)^(-1)) \desno|$. Međutim, determinanta umnoška jednaka je umnošku determinanti:

\[\lijevo| A\cdot B \desno|=\lijevo| A \desno|\cdot \lijevo| B \desno|\desna strelica \lijevo| A\cdot ((A)^(-1)) \desno|=\lijevo| A \desno|\cdot \lijevo| ((A)^(-1)) \desno|\]

Ali prema definiciji, $A\cdot ((A)^(-1))=E$, a determinanta $E$ uvijek je jednaka 1, pa

\[\begin(align) & A\cdot ((A)^(-1))=E; \\ & \lijevo| A\cdot ((A)^(-1)) \desno|=\lijevo| E\desno|; \\ & \lijevo| A \desno|\cdot \lijevo| ((A)^(-1)) \desno|=1. \\ \end(align)\]

Umnožak dvaju brojeva jednak je jedan samo ako svaki od tih brojeva nije nula:

\[\lijevo| A \right|\ne 0;\quad \lijevo| ((A)^(-1)) \right|\ne 0.\]

Dakle, ispada da je $\left| A \desno|\ne 0$. Lema je dokazana.

Zapravo, ovaj zahtjev je sasvim logičan. Sada ćemo analizirati algoritam za pronalaženje inverzne matrice - i postat će potpuno jasno zašto, s nultom determinantom, inverzna matrica u načelu ne može postojati.

Ali prvo, formulirajmo "pomoćnu" definiciju:

Definicija. Singularna matrica je kvadratna matrica veličine $\left[ n\times n \right]$ čija je determinanta nula.

Dakle, možemo tvrditi da je svaka invertibilna matrica nesingularna.

Kako pronaći inverz matrice

Sada ćemo razmotriti univerzalni algoritam za pronalaženje inverznih matrica. Općenito, postoje dva općeprihvaćena algoritma, a danas ćemo razmotriti i drugi.

Ona o kojoj ćemo sada raspravljati vrlo je učinkovita za matrice veličine $\left[ 2\times 2 \right]$ i - djelomično - veličine $\left[ 3\times 3 \right]$. Ali počevši od veličine $\left[ 4\times 4 \right]$ bolje je ne koristiti ga. Zašto - sada ćete sve shvatiti sami.

Algebarski dodaci

Pripremi se. Sada će biti boli. Ne, ne brinite: lijepa medicinska sestra u suknji, čarapama s čipkom neće vam doći i dati vam injekciju u zadnjicu. Sve je mnogo prozaičnije: algebarski dodaci i njezino veličanstvo "Union Matrix" dolaze vam.

Počnimo s glavnim. Neka postoji kvadratna matrica veličine $A=\left[ n\times n \right]$, čiji se elementi nazivaju $((a)_(ij))$. Zatim za svaki takav element možemo definirati algebarski komplement:

Definicija. Algebarski komplement $((A)_(ij))$ elementu $((a)_(ij))$ koji se nalazi u $i$tom retku i $j$tom stupcu matrice $A=\left[ n \times n \right]$ je konstrukcija oblika

\[((A)_(ij))=((\lijevo(-1 \desno))^(i+j))\cdot M_(ij)^(*)\]

Gdje je $M_(ij)^(*)$ determinanta matrice dobivena iz originalnog $A$ brisanjem istog $i$tog retka i $j$tog stupca.

Opet. Algebarski komplement elementu matrice s koordinatama $\left(i;j \right)$ označava se kao $((A)_(ij))$ i izračunava se prema shemi:

1. Prvo brišemo $i$-redak i $j$-ti stupac iz originalne matrice. Dobivamo novu kvadratnu matricu, a njezinu determinantu označavamo kao $M_(ij)^(*)$.
2. Zatim pomnožimo tu determinantu s $((\left(-1 \right))^(i+j))$ - isprva se ovaj izraz može činiti fantastičnim, ali u biti jednostavno shvaćamo znak ispred $M_(ij)^(*) $.
3. Brojimo i dobivamo konkretan broj. Oni. algebarsko zbrajanje je upravo broj, a ne neka nova matrica itd.

Sama matrica $M_(ij)^(*)$ naziva se dodatni minor elementu $((a)_(ij))$. I u tom smislu, gornja definicija algebarskog komplementa je poseban slučaj složenije definicije - ono što smo gledali u lekciji o determinanti.

Važna nota. Zapravo, u "odrasloj" matematici, algebarski dodaci definirani su na sljedeći način:

1. Uzimamo $k$ redaka i $k$ stupaca u kvadratnoj matrici. Na njihovom sjecištu dobivamo matricu veličine $\left[ k\times k \right]$ - njezina se determinanta naziva minor reda $k$ i označava se kao $((M)_(k))$.
2. Zatim prekrižimo ovih "odabranih" $k$ redaka i $k$ stupaca. Još jednom dobivate kvadratnu matricu - njezina se determinanta naziva dodatni minor i označava $M_(k)^(*)$.
3. Pomnožite $M_(k)^(*)$ s $((\left(-1 \right))^(t))$, gdje je $t$ (pozor!) zbroj brojeva svih odabranih redaka i stupci . Ovo će biti algebarsko zbrajanje.

Pogledajte treći korak: zapravo postoji zbroj od $2k$ pojmova! Druga stvar je da ćemo za $k=1$ dobiti samo 2 člana - to će biti isti $i+j$ - “koordinate” elementa $((a)_(ij))$ za koji smo tražeći algebarski komplement.

Dakle, danas koristimo malo pojednostavljenu definiciju. No, kako ćemo kasnije vidjeti, bit će i više nego dovoljno. Puno je bitnije sljedeće:

Definicija. Vezana matrica $S$ kvadratnoj matrici $A=\left[ n\times n \right]$ je nova matrica veličine $\left[ n\times n \right]$, koja se dobiva iz $A$ zamjenom $(( a)_(ij))$ algebarskim dodacima $((A)_(ij))$:

\\Rightarrow S=\left[ \begin(matrix) ((A)_(11)) & ((A)_(12)) & ... & ((A)_(1n)) \\ (( A)_(21)) & ((A)_(22)) & ... & ((A)_(2n)) \\ ... & ... & ... & ... \\ ((A)_(n1)) & ((A)_(n2)) & ... & ((A)_(nn)) \\\end(matrica) \desno]\]

Prva misao koja se javlja u trenutku spoznaje ove definicije je "koliko će se morati brojati!" Opustite se: morat ćete računati, ali ne toliko. :)

Pa, sve je to jako lijepo, ali zašto je potrebno? Ali zašto.

Glavni teorem

Vratimo se malo unatrag. Zapamtite, u lemi 3 je rečeno da je invertibilna matrica $A$ uvijek nesingularna (to jest, njena determinanta nije nula: $\left| A \right|\ne 0$).

Dakle, vrijedi i suprotno: ako matrica $A$ nije singularna, onda je uvijek invertibilna. Čak postoji i shema pretraživanja za $((A)^(-1))$. Provjerite:

Teorem o inverznoj matrici. Neka je dana kvadratna matrica $A=\left[ n\times n \right]$, a njena determinanta nije nula: $\left| A \desno|\ne 0$. Tada inverzna matrica $((A)^(-1))$ postoji i izračunava se po formuli:

\[((A)^(-1))=\frac(1)(\lijevo| A \desno|)\cdot ((S)^(T))\]

A sada - sve isto, ali čitljivim rukopisom. Da biste pronašli inverznu matricu, trebate:

1. Izračunajte determinantu $\left| A \right|$ i uvjerite se da nije nula.
2. Konstruirajte unijsku matricu $S$, tj. izbrojite 100500 algebarskih sabiraka $((A)_(ij))$ i postavite ih na mjesto $((a)_(ij))$.
3. Transponirajte ovu matricu $S$, a zatim je pomnožite s nekim brojem $q=(1)/(\left| A \right|)\;$.

To je sve! Pronađena je inverzna matrica $((A)^(-1))$. Pogledajmo primjere:

\[\lijevo[ \početak(matrica) 3 & 1 \\ 5 & 2 \\\kraj(matrica) \desno]\]

Riješenje. Provjerimo reverzibilnost. Izračunajmo determinantu:

\[\lijevo| A\desno|=\lijevo| \begin(matrix) 3 & 1 \\ 5 & 2 \\\end(matrix) \right|=3\cdot 2-1\cdot 5=6-5=1\]

Determinanta je različita od nule. To znači da je matrica invertibilna. Kreirajmo matricu unije:

Izračunajmo algebarske dodatke:

\[\begin(align) & ((A)_(11))=((\left(-1 \right))^(1+1))\cdot \left| 2 \desno|=2; \\ & ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| 5 \desno|=-5; \\ & ((A)_(21))=((\lijevo(-1 \desno))^(2+1))\cdot \lijevo| 1 \desno|=-1; \\ & ((A)_(22))=((\lijevo(-1 \desno))^(2+2))\cdot \lijevo| 3\desno|=3. \\ \end(align)\]

Obratite pažnju na: odrednice |2|, |5|, |1| i |3| su determinante matrica veličine $\left[ 1\times 1 \right]$, a ne moduli. Oni. Ako su u determinantama bili negativni brojevi, nema potrebe uklanjati “minus”.

Ukupno, naša sindikalna matrica izgleda ovako:

\[((A)^(-1))=\frac(1)(\lijevo| A \desno|)\cdot ((S)^(T))=\frac(1)(1)\cdot ( (\lijevo[ \početak(niz)(*(35)(r)) 2 & -5 \\ -1 & 3 \\\kraj(niz) \desno])^(T))=\lijevo[ \početak (niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\kraj (niz) \desno]\]

OK, sada je sve gotovo. Problem je riješen.

Odgovor. $\lijevo[ \begin(niz)(*(35)(r)) 2 & -1 \\ -5 & 3 \\\end(niz) \desno]$

Zadatak. Nađi inverznu matricu:

\[\lijevo[ \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \desno] \]

Riješenje. Ponovno izračunavamo determinantu:

\[\begin(align) & \left| \begin(niz)(*(35)(r)) 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end(niz) \right|=\begin(matrica ) \lijevo(1\cdot 2\cdot 1+\lijevo(-1 \desno)\cdot \lijevo(-1 \desno)\cdot 1+2\cdot 0\cdot 0 \desno)- \\ -\lijevo (2\cdot 2\cdot 1+\lijevo(-1 \desno)\cdot 0\cdot 1+1\cdot \lijevo(-1 \desno)\cdot 0 \desno) \\\end(matrica)= \ \ & =\lijevo(2+1+0 \desno)-\lijevo(4+0+0 \desno)=-1\ne 0. \\ \end(align)\]

Determinanta je različita od nule - matrica je invertibilna. Ali sada će biti jako teško: trebamo izbrojati čak 9 (devet, jebem ti mater!) algebarskih zbrajanja. I svaki od njih će sadržavati determinantu $\left[ 2\times 2 \right]$. Letio:

\[\begin(matrica) ((A)_(11))=((\lijevo(-1 \desno))^(1+1))\cdot \lijevo| \početak(matrica) 2 & -1 \\ 0 & 1 \\\kraj(matrica) \desno|=2; \\ ((A)_(12))=((\lijevo(-1 \desno))^(1+2))\cdot \lijevo| \begin(matrica) 0 & -1 \\ 1 & 1 \\\end(matrica) \right|=-1; \\ ((A)_(13))=((\lijevo(-1 \desno))^(1+3))\cdot \lijevo| \početak(matrica) 0 & 2 \\ 1 & 0 \\\kraj(matrica) \desno|=-2; \\ ... \\ ((A)_(33))=((\lijevo(-1 \desno))^(3+3))\cdot \lijevo| \početak(matrica) 1 & -1 \\ 0 & 2 \\\kraj(matrica) \desno|=2; \\ \kraj(matrica)\]

Ukratko, matrica unije će izgledati ovako:

Stoga će inverzna matrica biti:

\[((A)^(-1))=\frac(1)(-1)\cdot \left[ \begin(matrix) 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end(matrica) \right]=\left[ \begin(array)(*(35)(r))-2 & -1 & 3 \\ 1 & 1 & -1 \ \2 & 1 & -2 \\\end(niz) \desno]\]

To je to. Evo odgovora.

Odgovor. $\lijevo[ \begin(niz)(*(35)(r)) -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end(niz) \desno ]$

Kao što vidite, na kraju svakog primjera izvršili smo provjeru. S tim u vezi, važna napomena:

Nemojte biti lijeni provjeriti. Pomnožite izvornu matricu s pronađenom inverznom matricom - trebali biste dobiti $E$.

Provođenje ove provjere puno je lakše i brže od traženja greške u daljnjim izračunima kada, na primjer, rješavate matričnu jednadžbu.

Alternativni način

Kao što sam rekao, teorem o inverznoj matrici radi izvrsno za veličine $\left[ 2\times 2 \right]$ i $\left[ 3\times 3 \right]$ (u potonjem slučaju nije tako "sjajno" " ), ali za veće matrice tuga počinje.

Ali ne brinite: postoji alternativni algoritam s kojim možete mirno pronaći inverz čak i za matricu $\left[ 10\times 10 \right]$. No, kao što se često događa, za razmatranje ovog algoritma treba nam malo teorijske pozadine.

Elementarne transformacije

Među svim mogućim transformacijama matrica postoji nekoliko posebnih - nazivaju se elementarnim. Postoje točno tri takve transformacije:

1. Množenje. Možete uzeti $i$-ti redak (stupac) i pomnožiti ga s bilo kojim brojem $k\ne 0$;
2. Dodatak. Dodajte $i$-tom retku (stupcu) bilo koji drugi $j$-ti redak (stupac) pomnožen s bilo kojim brojem $k\ne 0$ (možete, naravno, učiniti $k=0$, ali što je točka? ? Ništa se neće promijeniti).
3. Preuređenje. Uzmite $i$-ti i $j$-ti red (kolone) i zamijenite mjesta.

Zašto se te transformacije nazivaju elementarnim (za velike matrice ne izgledaju tako elementarno) i zašto ih ima samo tri - ova su pitanja izvan opsega današnje lekcije. Stoga nećemo ulaziti u detalje.

Još jedna stvar je važna: sve te perverzije moramo izvesti na adjungiranoj matrici. Da, da: dobro ste čuli. Sada će biti još jedna definicija - posljednja u današnjoj lekciji.

Adjungirana matrica

Sigurno ste u školi rješavali sustave jednadžbi metodom zbrajanja. Pa, evo, oduzmite drugu od jedne linije, pomnožite neku liniju s brojem - to je sve.

Dakle: sada će sve biti isto, ali na “odrastao” način. Spreman?

Definicija. Neka su zadane matrica $A=\lijevo[ n\puta n \desno]$ i matrica identiteta $E$ iste veličine $n$. Zatim adjungirana matrica $\left[ A\left| E \ desno. \right]$ je nova matrica veličine $\left[ n\times 2n \right]$ koja izgleda ovako:

\[\lijevo[ A\lijevo| E \ desno. \desno]=\lijevo[ \begin(niz)(rrrr|rrrr)((a)_(11)) & ((a)_(12)) & ... & ((a)_(1n)) & 1 & 0 & ... & 0 \\((a)_(21)) & ((a)_(22)) & ... & ((a)_(2n)) & 0 & 1 & ... & 0 \\... & ... & ... & ... & ... & ... & ... & ... & ... \\((a)_(n1)) & ((a)_(n2)) & ... & ((a)_(nn)) & 0 & 0 & ... & 1 \\\end(array) \right]\]

Ukratko, uzmemo matricu $A$, s desne strane joj dodijelimo matricu identiteta $E$ tražene veličine, odvajamo ih okomitom trakom radi ljepote - evo vam adjoint. :)

U čemu je kvaka? Evo što:

Teorema. Neka je matrica $A$ invertibilna. Razmotrimo adjungiranu matricu $\left[ A\left| E \ desno. \desno]$. Ako koristite elementarne pretvorbe nizova dovesti ga u oblik $\left[ E\left| Svijetao. \right]$, tj. množenjem, oduzimanjem i preuređivanjem redaka da se iz $A$ dobije matrica $E$ s desne strane, tada je matrica $B$ dobivena s lijeve strane inverzna od $A$:

\[\lijevo[ A\lijevo| E \ desno. \desno]\na \lijevo[ E\lijevo| Svijetao. \desno]\desna strelica B=((A)^(-1))\]

Tako je jednostavno! Ukratko, algoritam za pronalaženje inverzne matrice izgleda ovako:

1. Napišite adjungiranu matricu $\left[ A\left| E \ desno. \desno]$;
2. Izvršite elementarne konverzije nizova dok se $E$ ne pojavi umjesto $A$;
3. Naravno, nešto će se pojaviti i s lijeve strane - određena matrica $B$. Ovo će biti suprotno;
4. DOBIT!:)

Naravno, ovo je puno lakše reći nego učiniti. Dakle, pogledajmo nekoliko primjera: za veličine $\left[ 3\times 3 \right]$ i $\left[ 4\times 4 \right]$.

Zadatak. Nađi inverznu matricu:

\[\lijevo[ \begin(niz)(*(35)(r)) 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end(niz) \desno]\ ]

Riješenje. Kreiramo adjungiranu matricu:

\[\lijevo[ \begin(niz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end(niz) \desno]\]

Budući da je posljednji stupac izvorne matrice ispunjen jedinicama, oduzmite prvi red od ostatka:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & - 2 & 1 & 0 & 0 & 1 \\\end(niz) \desno]\početak(matrica) \downarrow \\ -1 \\ -1 \\\kraj(matrica)\to \\ & \to \lijevo [ \početak(niz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Nema više jedinica, osim prve linije. Ali ne diramo ga, inače će se novouklonjene jedinice početi "množiti" u trećem stupcu.

Ali drugu liniju možemo oduzeti dva puta od zadnje - dobit ćemo jednu u donjem lijevom kutu:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end(niz) \desno]\početak(matrica) \ \\ \strelica prema dolje \\ -2 \\\kraj(matrica)\do \\ & \lijevo [ \početak(niz)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(array) \right] \\ \end(align)\]

Sada možemo oduzeti zadnji red od prvog i dvaput od drugog - na ovaj način "nuliramo" prvi stupac:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno]\početak(matrica) -1 \\ -2 \\ \strelica prema gore \\\kraj(matrica)\do \\ & \ na \lijevo[ \begin(niz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno] \\ \end(poravnaj)\]

Pomnožite drugi redak s −1, a zatim ga oduzmite 6 puta od prvog i dodajte 1 put posljednjem:

\[\begin(align) & \left[ \begin(array)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \ \ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \ \\\end(matrica)\to \\ & \to \lijevo[ \begin(niz)(rrr|rrr) 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end(niz) \desno]\početak(matrica) -6 \\ \updownarrow \\ +1 \\\end (matrica)\to \\ & \to \lijevo[ \begin(niz)(rrr|rrr) 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end(niz) \desno] \\ \end(align)\]

Sve što preostaje je zamijeniti retke 1 i 3:

\[\lijevo[ \begin(niz)(rrr|rrr) 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & - 18 & 32 & -13 \\\end(niz) \desno]\]

Spreman! Desno je tražena inverzna matrica.

Odgovor. $\lijevo[ \begin(niz)(*(35)(r))4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end(niz) \desno ]$

Zadatak. Nađi inverznu matricu:

\[\lijevo[ \begin(matrix) 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\kraj(matrica) \desno]\]

Riješenje. Ponovno sastavljamo adjungt:

\[\lijevo[ \begin(niz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \ \ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right]\]

Isplačimo se malo, rastužimo se koliko sada moramo brojati... i počnemo brojati. Prvo, "izbrišite" prvi stupac oduzimanjem reda 1 od redaka 2 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(niz) \right]\begin(matrica) \downarrow \\ -1 \\ -1 \\ \ \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end(array) \right] \\ \end(align)\]

Vidimo previše "protiv" u recima 2-4. Pomnožite sva tri retka s −1, a zatim spalite treći stupac oduzimanjem retka 3 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & - 1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\ \end(niz) \desno]\početak(matrica) \ \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\ \lijevo| \cdot \lijevo(-1 \desno) \desno. \\\end(matrica)\to \\ & \na \lijevo[ \begin(niz)(rrrr|rrrr) 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & ​​​​1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\ \end (niz) \desno]\begin(matrica) -2 \\ -1 \\ \updownarrow \\ -2 \\\end(matrica)\to \\ & \to \left[ \begin(niz)( rrrr| rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

Sada je vrijeme da "spržite" posljednji stupac originalne matrice: oduzmite liniju 4 od ostatka:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz ) \right]\begin(matrica) +1 \\ -3 \\ -2 \\ \uparrow \\\end(matrix)\to \\ & \to \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

Završno bacanje: "spalite" drugi stupac oduzimanjem reda 2 od redaka 1 i 3:

\[\begin(align) & \left[ \begin(array)(rrrr|rrrr) 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end( niz) \desno]\početak(matrica) 6 \\ \updownarrow \\ -5 \\ \ \\\end(matrica)\to \\ & \na \lijevo[ \početak(niz)(rrrr|rrrr) 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end(niz) \desno] \\ \end(align)\]

I opet je matrica identiteta lijevo, što znači da je inverz desno. :)

Odgovor. $\lijevo[ \begin(matrica) 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & - 1 \\\end(matrica) \desno]$

OK, sada je sve gotovo. Provjerite sami - sjeban sam. :)

Matrica $A^(-1)$ naziva se inverzom kvadratne matrice $A$ ako je zadovoljen uvjet $A^(-1)\cdot A=A\cdot A^(-1)=E$, gdje je $E $ matrica identiteta, čiji je red jednak redu matrice $A$.

Nesingularna matrica je matrica čija determinanta nije jednaka nuli. Prema tome, singularna matrica je ona čija je determinanta jednaka nuli.

Inverzna matrica $A^(-1)$ postoji ako i samo ako je matrica $A$ nesingularna. Ako inverzna matrica $A^(-1)$ postoji, onda je ona jedinstvena.

Postoji nekoliko načina da se pronađe inverz matrice, a mi ćemo pogledati dva od njih. Na ovoj stranici raspravljat će se o metodi adjungirane matrice, koja se smatra standardnom u većini tečajeva više matematike. U drugom dijelu govori se o drugoj metodi pronalaženja inverzne matrice (metodi elementarnih transformacija), koja uključuje korištenje Gaussove metode ili Gauss-Jordanove metode.

Metoda adjungirane matrice

Neka je dana matrica $A_(n\puta n)$. Da bi se pronašla inverzna matrica $A^(-1)$, potrebna su tri koraka:

1. Nađite determinantu matrice $A$ i uvjerite se da je $\Delta A\neq 0$, tj. da je matrica A nesingularna.
2. Sastavite algebarske komplemente $A_(ij)$ svakog elementa matrice $A$ i napišite matricu $A_(n\times n)^(*)=\left(A_(ij) \right)$ iz pronađene algebarske nadopunjuje.
3. Napišite inverznu matricu uzimajući u obzir formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$.

Matrica $(A^(*))^T$ često se naziva pridružena (recipročna, saveznička) matrici $A$.

Ako se rješenje radi ručno, tada je prva metoda dobra samo za matrice relativno malih redova: druga (), treća (), četvrta (). Da bi se pronašao inverz matrice višeg reda, koriste se druge metode. Na primjer, Gaussova metoda, o kojoj se govori u drugom dijelu.

Primjer br. 1

Pronađite inverziju matrice $A=\left(\begin(array) (cccc) 5 & -4 &1 & 0 \\ 12 &-11 &4 & 0 \\ -5 & 58 &4 & 0 \\ 3 & - 1 & -9 & 0 \end(array) \right)$.

Kako su svi elementi četvrtog stupca jednaki nuli, onda je $\Delta A=0$ (tj. matrica $A$ je singularna). Budući da je $\Delta A=0$, ne postoji matrica inverzna matrici $A$.

Odgovor: matrica $A^(-1)$ ne postoji.

Primjer br. 2

Pronađite inverz matrice $A=\left(\begin(array) (cc) -5 & 7 \\ 9 & 8 \end(array)\right)$. Izvršite provjeru.

Koristimo metodu adjungirane matrice. Najprije pronađimo determinantu zadane matrice $A$:

$$ \Delta A=\lijevo| \begin(niz) (cc) -5 & 7\\ 9 & 8 \end(niz)\right|=-5\cdot 8-7\cdot 9=-103. $$

Budući da je $\Delta A \neq 0$, tada inverzna matrica postoji, stoga ćemo nastaviti s rješavanjem. Pronalaženje algebarskih komplemenata

\begin(aligned) & A_(11)=(-1)^2\cdot 8=8; \; A_(12)=(-1)^3\cdot 9=-9;\\ & A_(21)=(-1)^3\cdot 7=-7; \; A_(22)=(-1)^4\cdot (-5)=-5.\\ \end(poravnano)

Sastavljamo matricu algebarskih sabiranja: $A^(*)=\left(\begin(array) (cc) 8 & -9\\ -7 & -5 \end(array)\right)$.

Transponiramo dobivenu matricu: $(A^(*))^T=\left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array)\right)$ (the rezultirajuća matrica se često naziva pridružena ili pridružena matrica matrici $A$). Koristeći formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, imamo:

$$ A^(-1)=\frac(1)(-103)\cdot \lijevo(\begin(niz) (cc) 8 & -7\\ -9 & -5 \end(niz)\desno) =\lijevo(\početak(niz) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \kraj(niz)\desno) $$

Dakle, inverzna matrica je pronađena: $A^(-1)=\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \end(array )\desno) $. Za provjeru istinitosti rezultata dovoljno je provjeriti istinitost jedne od jednakosti: $A^(-1)\cdot A=E$ ili $A\cdot A^(-1)=E$. Provjerimo jednakost $A^(-1)\cdot A=E$. Kako bismo manje radili s razlomcima, zamijenit ćemo matricu $A^(-1)$ ne u obliku $\left(\begin(array) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \ end(array)\right)$, i u obliku $-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end(array )\right)$:

$$ A^(-1)\cdot(A) =-\frac(1)(103)\cdot \left(\begin(array) (cc) 8 & -7\\ -9 & -5 \end( niz)\desno)\cdot\lijevo(\početak(niz) (cc) -5 & 7 \\ 9 & 8 \kraj(niz)\desno) =-\frac(1)(103)\cdot\lijevo( \begin(array) (cc) -103 & 0 \\ 0 & -103 \end(array)\right) =\left(\begin(array) (cc) 1 & 0 \\ 0 & 1 \end(array) )\desno) =E $$

Odgovor: $A^(-1)=\lijevo(\početak(niz) (cc) -8/103 & 7/103\\ 9/103 & 5/103 \kraj(niz)\desno)$.

Primjer br. 3

Pronađite inverznu matricu za matricu $A=\left(\begin(array) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(array) \right)$ . Izvršite provjeru.

Počnimo s izračunavanjem determinante matrice $A$. Dakle, determinanta matrice $A$ je:

$$ \Delta A=\lijevo| \begin(niz) (ccc) 1 & 7 & 3 \\ -4 & 9 & 4 \\ 0 & 3 & 2\end(niz) \right| = 18-36+56-12=26. $$

Budući da je $\Delta A\neq 0$, tada inverzna matrica postoji, stoga ćemo nastaviti s rješavanjem. Pronalazimo algebarske komplemente svakog elementa zadane matrice:

$$ \begin(aligned) & A_(11)=(-1)^(2)\cdot\left|\begin(array)(cc) 9 & 4\\ 3 & 2\end(array)\right| =6;\; A_(12)=(-1)^(3)\cdot\lijevo|\početak(niz)(cc) -4 &4 \\ 0 & 2\kraj(niz)\desno|=8;\; A_(13)=(-1)^(4)\cdot\lijevo|\begin(niz)(cc) -4 & 9\\ 0 & 3\end(niz)\desno|=-12;\\ & A_(21)=(-1)^(3)\cdot\lijevo|\početak(niz)(cc) 7 & 3\\ 3 & 2\kraj(niz)\desno|=-5;\; A_(22)=(-1)^(4)\cdot\lijevo|\početak(niza)(cc) 1 & 3\\ 0 & 2\kraj(niza)\desno|=2;\; A_(23)=(-1)^(5)\cdot\lijevo|\begin(niz)(cc) 1 & 7\\ 0 & 3\end(niz)\desno|=-3;\\ & A_ (31)=(-1)^(4)\cdot\lijevo|\begin(niz)(cc) 7 & 3\\ 9 & 4\end(niz)\desno|=1;\; A_(32)=(-1)^(5)\cdot\lijevo|\begin(niz)(cc) 1 & 3\\ -4 & 4\end(niz)\desno|=-16;\; A_(33)=(-1)^(6)\cdot\lijevo|\begin(niz)(cc) 1 & 7\\ -4 & 9\end(niz)\desno|=37. \kraj(poravnano) $$

Sastavljamo matricu algebarskih sabiranja i transponiramo je:

$$ A^*=\lijevo(\početak(niza) (ccc) 6 & 8 & -12 \\ -5 & 2 & -3 \\ 1 & -16 & 37\kraj(niza) \desno); \; (A^*)^T=\lijevo(\početak(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\kraj (niz) \desno) . $$

Koristeći formulu $A^(-1)=\frac(1)(\Delta A)\cdot (A^(*))^T$, dobivamo:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array) \right)= \left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \ \ -6/13 & -3/26 & 37/26 \end(array) \right) $$

Dakle, $A^(-1)=\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ - 6 /13 & -3/26 & 37/26 \end(array) \right)$. Za provjeru istinitosti rezultata dovoljno je provjeriti istinitost jedne od jednakosti: $A^(-1)\cdot A=E$ ili $A\cdot A^(-1)=E$. Provjerimo jednakost $A\cdot A^(-1)=E$. Kako bismo manje radili s razlomcima, zamijenit ćemo matricu $A^(-1)$ ne u obliku $\left(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \ \ 4/13 & 1/13 & -8/13 \\ -6/13 & -3/26 & 37/26 \end(array) \right)$, i u obliku $\frac(1)(26 )\cdot \lijevo( \begin(niz) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(niz) \desno)$:

$$ A\cdot(A^(-1)) =\left(\begin(array)(ccc) 1 & 7 & 3 \\ -4 & 9 & 4\\ 0 & 3 & 2\end(array) \desno)\cdot \frac(1)(26)\cdot \lijevo(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\ kraj(niz) \desno) =\frac(1)(26)\cdot\lijevo(\početak(niz) (ccc) 26 & 0 & 0 \\ 0 & 26 & 0 \\ 0 & 0 & 26\kraj (niz) \desno) =\lijevo(\početak(niz) (ccc) 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end(niz) \desno) =E $$

Provjera je bila uspješna, inverzna matrica $A^(-1)$ je ispravno pronađena.

Odgovor: $A^(-1)=\lijevo(\begin(array) (ccc) 3/13 & -5/26 & 1/26 \\ 4/13 & 1/13 & -8/13 \\ -6 /13 & -3/26 & 37/26 \end(array) \right)$.

Primjer br. 4

Pronađite matricu inverznu od matrice $A=\left(\begin(array) (cccc) 6 & -5 & 8 & 4\\ 9 & 7 & 5 & 2 \\ 7 & 5 & 3 & 7\\ -4 & 8 & -8 & -3 \end(array) \right)$.

Za matricu četvrtog reda, pronalaženje inverzne matrice korištenjem algebarskih adicija donekle je teško. Međutim, takvi se primjeri javljaju u ispitnim radovima.

Da biste pronašli inverz matrice, prvo morate izračunati determinantu matrice $A$. Najbolji način da to učinite u ovoj situaciji je rastavljanjem determinante duž retka (stupca). Odaberemo bilo koji redak ili stupac i pronađemo algebarske komplemente svakog elementa odabranog retka ili stupca.

Na primjer, za prvi redak dobivamo:

$$ A_(11)=\lijevo|\početak(niza)(ccc) 7 & 5 & 2\\ 5 & 3 & 7\\ 8 & -8 & -3 \kraj(niza)\desno|=556; \; A_(12)=-\lijevo|\početak(niz)(ccc) 9 & 5 & 2\\ 7 & 3 & 7 \\ -4 & -8 & -3 \kraj(niz)\desno|=-300 ; $$ $$ A_(13)=\lijevo|\begin(niz)(ccc) 9 & 7 & 2\\ 7 & 5 & 7\\ -4 & 8 & -3 \end(niz)\desno|= -536;\; A_(14)=-\lijevo|\početak(niz)(ccc) 9 & 7 & 5\\ 7 & 5 & 3\\ -4 & 8 & -8 \kraj(niz)\desno|=-112. $$

Determinanta matrice $A$ izračunava se pomoću sljedeće formule:

$$ \Delta(A)=a_(11)\cdot A_(11)+a_(12)\cdot A_(12)+a_(13)\cdot A_(13)+a_(14)\cdot A_(14 )=6\cdot 556+(-5)\cdot(-300)+8\cdot(-536)+4\cdot(-112)=100. $$

$$ \begin(aligned) & A_(21)=-77;\;A_(22)=50;\;A_(23)=87;\;A_(24)=4;\\ & A_(31) =-93;\;A_(32)=50;\;A_(33)=83;\;A_(34)=36;\\ & A_(41)=473;\;A_(42)=-250 ;\;A_(43)=-463;\;A_(44)=-96. \kraj(poravnano) $$

Matrica algebarskih komplemenata: $A^*=\left(\begin(array)(cccc) 556 & -300 & -536 & -112\\ -77 & 50 & 87 & 4 \\ -93 & 50 & 83 & 36\\ 473 & -250 & -463 & -96\end(array)\right)$.

Adjungirana matrica: $(A^*)^T=\left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96\end(array)\right)$.

Inverzna matrica:

$$ A^(-1)=\frac(1)(100)\cdot \left(\begin(array) (cccc) 556 & -77 & -93 & 473\\ -300 & 50 & 50 & -250 \\ -536 & 87 & 83 & -463\\ -112 & 4 & 36 & -96 \end(niz) \right)= \lijevo(\begin(niz) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/ 25 & 1/25 & 9/25 & -24/25 \end(array) \right) $$

Provjeru, po želji, možete izvršiti na isti način kao u prethodnim primjerima.

Odgovor: $A^(-1)=\lijevo(\begin(array) (cccc) 139/25 & -77/100 & -93/100 & 473/100 \\ -3 & 1/2 & 1/2 & -5/2 \\ -134/25 & 87/100 & 83/100 & -463/100 \\ -28/25 & 1/25 & 9/25 & -24/25 \end(niz) \desno) $.

U drugom dijelu ćemo razmotriti još jedan način pronalaska inverzne matrice, koji uključuje korištenje transformacija Gaussove metode ili Gauss-Jordanove metode.

Metode za pronalaženje inverzne matrice. Razmotrimo kvadratnu matricu

Označimo Δ = det A.

Kvadratna matrica A naziva se nedegeneriran, ili nije posebno, ako je njegova determinanta različita od nule, i degenerirati, ili poseban, AkoΔ = 0.

Kvadratna matrica B je za kvadratnu matricu A istog reda ako je njihov umnožak A B = B A = E, gdje je E matrica identiteta istog reda kao matrice A i B.

Teorema . Da bi matrica A imala inverznu matricu potrebno je i dovoljno da njena determinanta bude različita od nule.

Inverzna matrica matrice A, označena s A- 1, pa je B = A - 1 a izračunava se po formuli

, (1)

gdje su A i j algebarski komplementi elemenata a i j matrice A..

Izračunavanje A -1 pomoću formule (1) za matrice visokog reda vrlo je zahtjevno, pa je u praksi zgodno pronaći A -1 pomoću metode elementarnih transformacija (ET). Svaka nesingularna matrica A može se reducirati na matricu identiteta E primjenom samo stupaca (ili samo redaka) na matricu identiteta. Ako se transformacije savršene nad matricom A primjenjuju istim redom na matricu identiteta E, rezultat će biti inverzna matrica. Pogodno je izvesti EP na matricama A i E istovremeno, pišući obje matrice jednu do druge kroz crtu. Napomenimo još jednom da kada tražite kanonski oblik matrice, da biste ga pronašli, možete koristiti transformacije redaka i stupaca. Ako trebate pronaći inverziju matrice, trebali biste koristiti samo retke ili samo stupce tijekom procesa transformacije.

Primjer 1. Za matricu nađi A -1 .

Riješenje.Prvo nalazimo determinantu matrice A
To znači da inverzna matrica postoji i možemo je pronaći pomoću formule: , gdje su A i j (i,j=1,2,3) algebarski dodaci elemenata a i j izvorne matrice.

Gdje .

Primjer 2. Metodom elementarnih transformacija pronađite A -1 za matricu: A = .

Riješenje.Originalnoj matrici s desne strane pridružujemo matricu identiteta istog reda: . Koristeći elementarne transformacije stupaca, lijevu ćemo “polovicu” svesti na onu identiteta, istovremeno izvodeći potpuno iste transformacije na desnoj matrici.
Da biste to učinili, zamijenite prvi i drugi stupac: ~ . Trećem stupcu dodamo prvi, a drugom - prvi, pomnožen s -2: . Od prvog stupca oduzimamo drugi udvostručeni, a od trećeg - drugi pomnožen sa 6; . Dodajmo treći stupac prvom i drugom: . Pomnožite zadnji stupac s -1: . Kvadratna matrica dobivena desno od okomite trake je inverzna matrica zadane matrice A. Dakle,
.