Other

The range of functions in USE problems. Lesson topic: “The set of function values in Unified State Examination problems How to indicate the set of function values

A function is a model. Let's define X as a set of values of an independent variable // independent means any.

A function is a rule with the help of which, for each value of the independent variable from the set X, one can find a unique value of the dependent variable. // i.e. for every x there is one y.

From the definition it follows that there are two concepts - an independent variable (which we denote by x and it can take any value) and a dependent variable (which we denote by y or f (x) and it is calculated from the function when we substitute x).

FOR EXAMPLE y=5+x

1. Independent is x, which means we take any value, let x=3

2. Now let’s calculate y, which means y=5+x=5+3=8. (y depends on x, because whatever x we substitute, we get the same y)

The variable y is said to functionally depend on the variable x and is denoted as follows: y = f (x).

FOR EXAMPLE.

1.y=1/x. (called hyperbole)

2. y=x^2. (called parabola)

3.y=3x+7. (called straight line)

4. y= √ x. (called parabola branch)

The independent variable (which we denote by x) is called the function argument.

Function Domain

The set of all values that a function argument takes is called the function's domain and is denoted D(f) or D(y).

Consider D(y) for 1.,2.,3.,4.

1. D (y)= (∞; 0) and (0;+∞) //the entire set of real numbers except zero.

2. D (y)= (∞; +∞)//all number of real numbers

3. D (y)= (∞; +∞)//all number of real numbers

4. D (y) = .

1) y = cos 2x 2) y = sin 2 x 3) y = cos 2 x +2

4) y = 2 sin 4 x

6. Find the set of function valuesy = tg 2 xon the segment

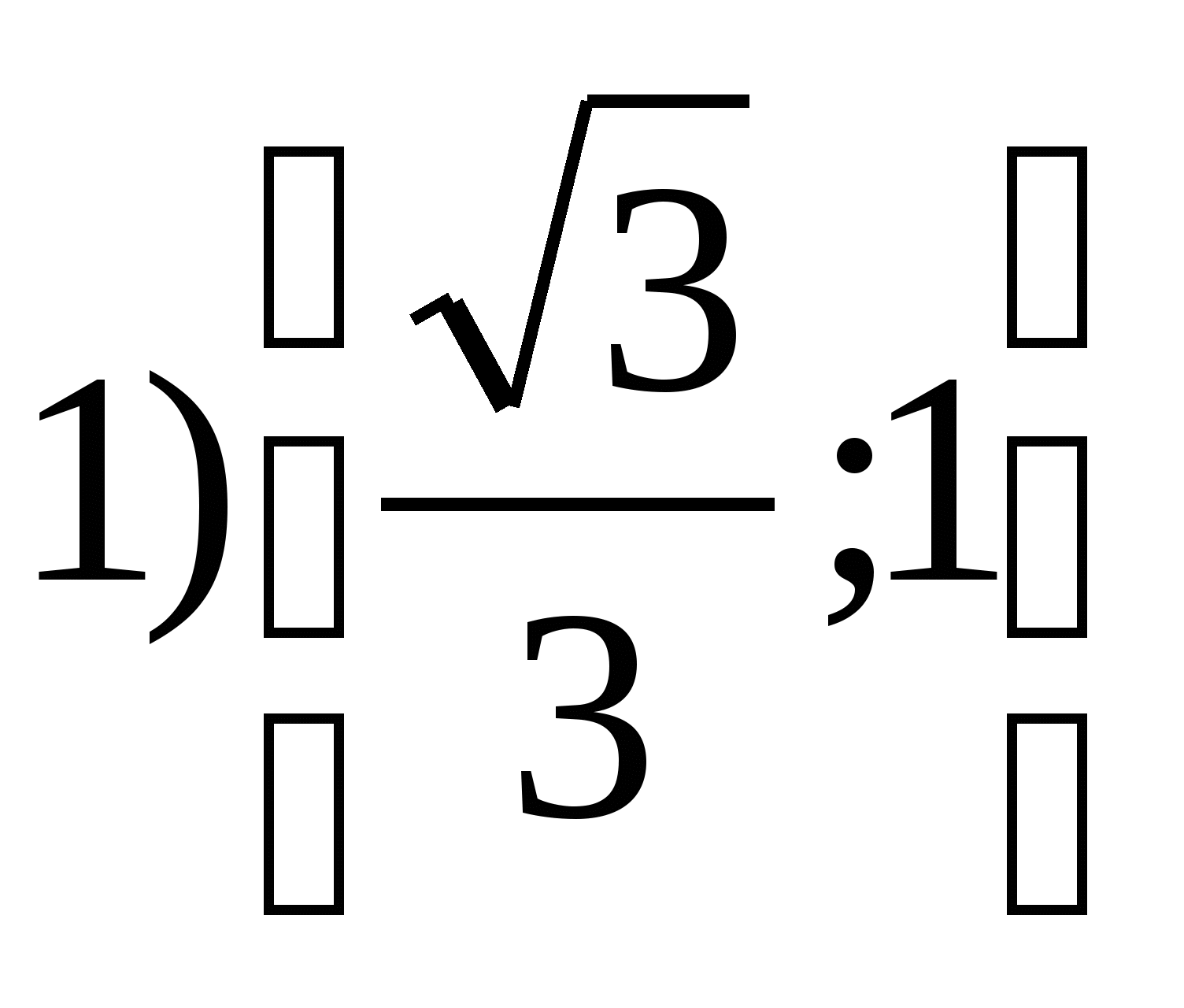
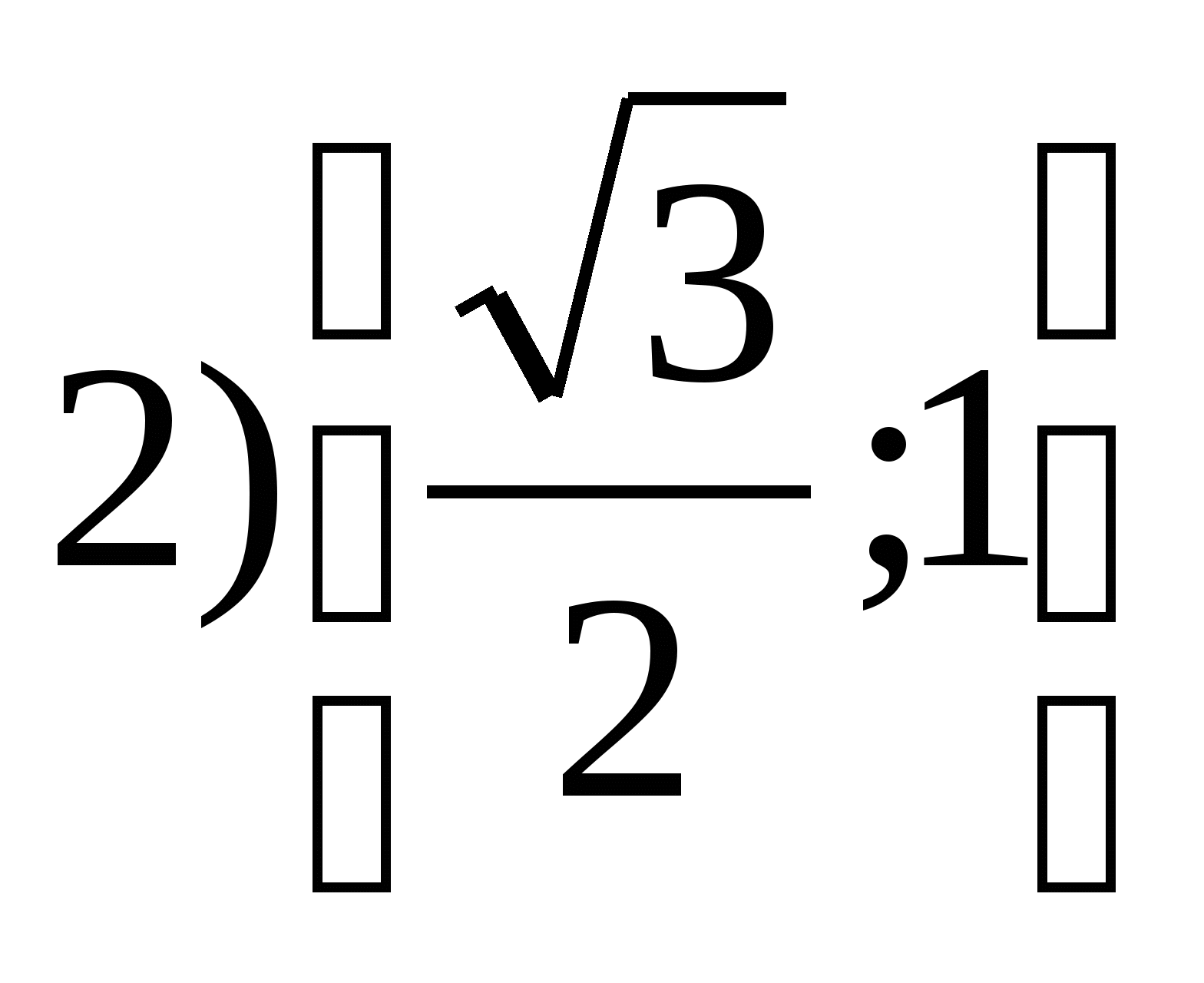
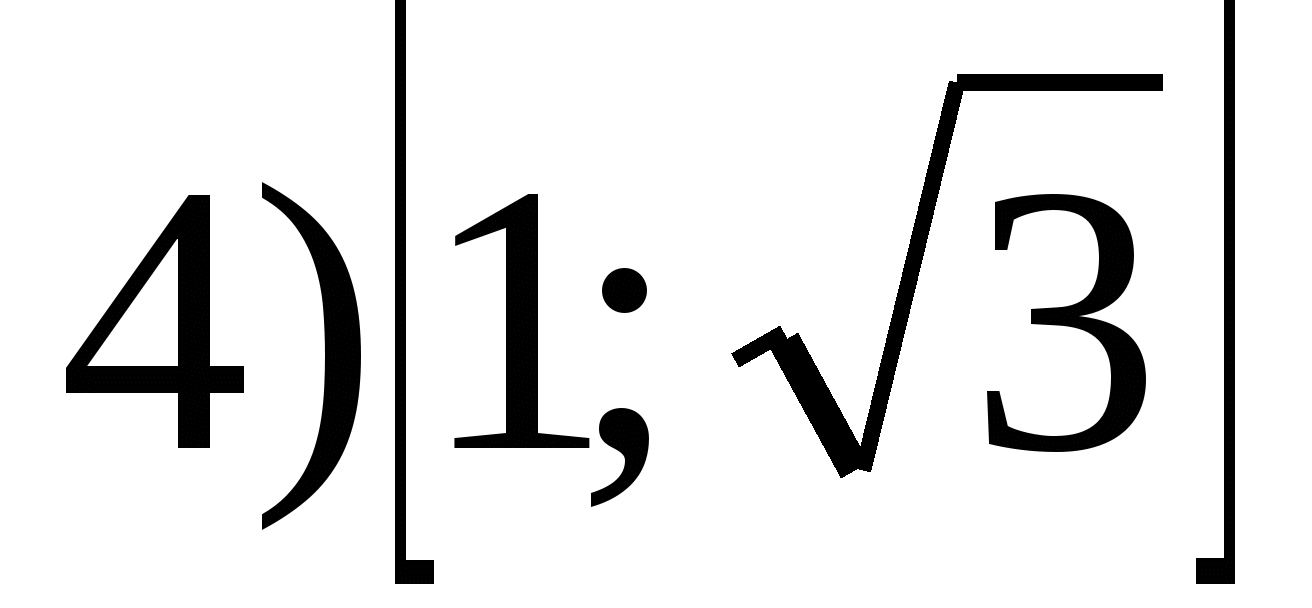
7. Find the sum of all integers that are included in the range of the functiony = 4 cos 2 x – 7.

1) -25 2) 25 3) -22 4) 0

Option 2

y = 2 cos 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Find the range of the function

1) 3) (-∞;∞) 4) .

3. Specify the smallest number in the function range

1) 4 2) -3 3) 1 4) -7

4. Specify the largest integer in the function range

1) 2 2) 13 3) 12 4) -2

5. Specify a function whose set of values is the segment [-5;5].

1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. Find the set of function values
on the segment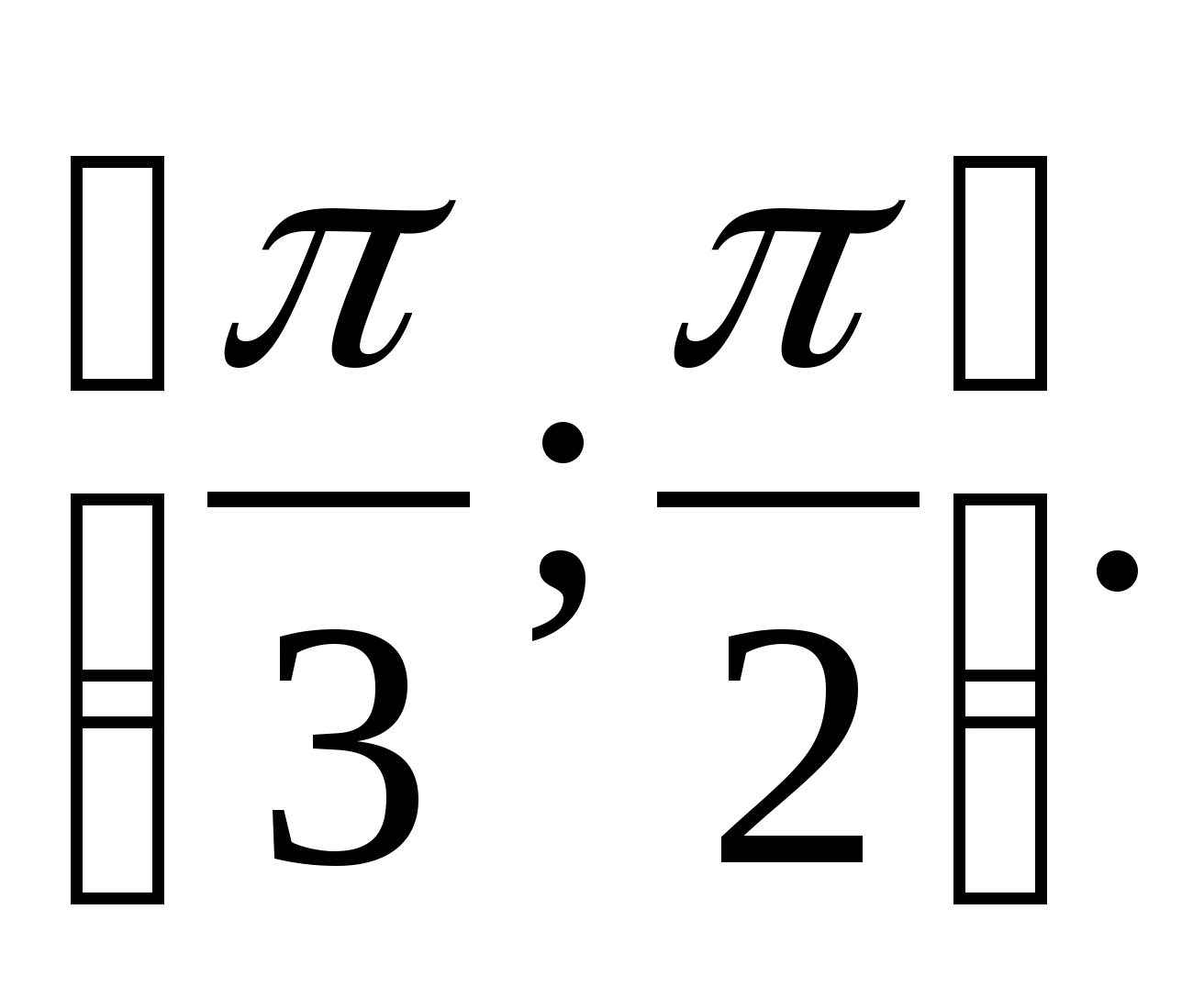

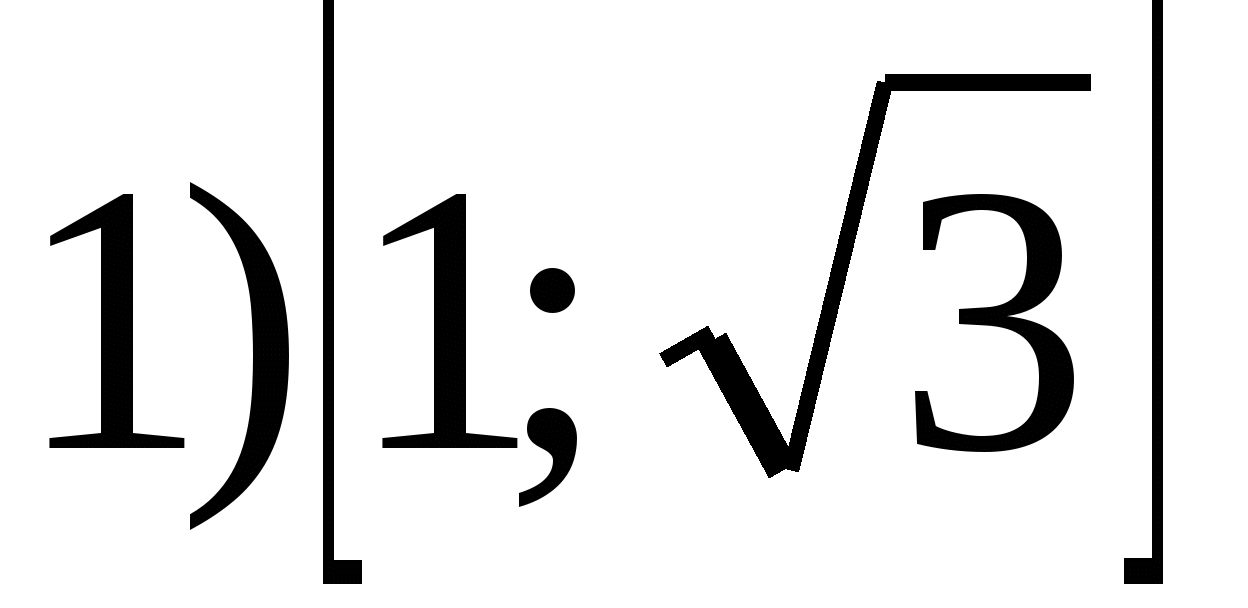
7. Find the product of all integers that are included in the range of values of the function y = 5 – 3sin 2 x.

1) 120 2) 14 3) -15 4) 0

Option 3
1. Specify a set of function valuesy = sin 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Specify the smallest number from the range of values of the function y = 5tg 2 x+2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. Specify a function whose set of values is a segment

[-17;-13].

1) y = 5 sin x – 8 3) y = -cos x +15

2) y = 2 cos x – 15 4) y = 3 sin x +10

6. Specify the smallest natural number that is not included in the set of function values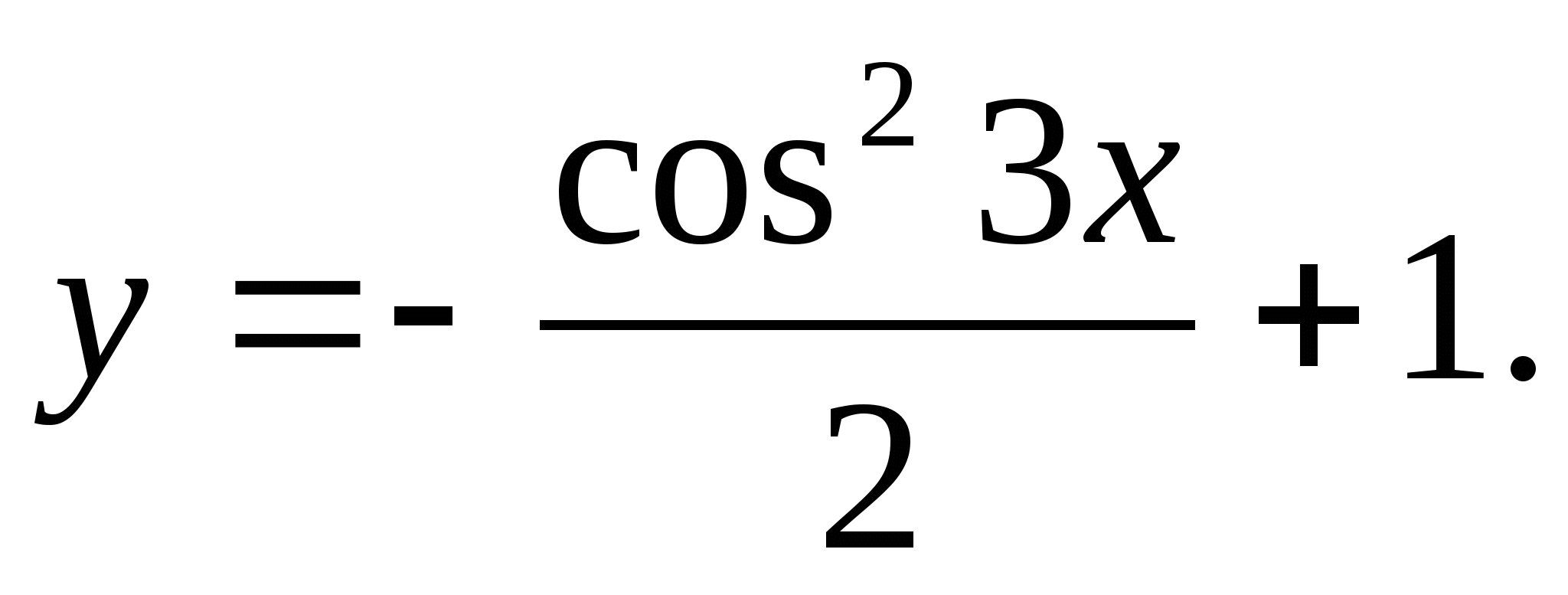

1) 2 2) 4 3) 15 4) 6

7. How many integers belong to the set of function values

y = 2 cos 3 x +10?

1) 2 2) 3 3) 4 5) 5

Option 4

1) 2) 4) (-7;-6)

2. Find the range of the function

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Specify the largest number in the function rangey = -3 ctg 2 x+7.

1) 10 2) 4 3) 7 4) -3

4. Which of the following numbers is not included in the set of function values

1) -6 2) -5 3) -10 4) -7

5. Specify a function whose set of values is the segment.

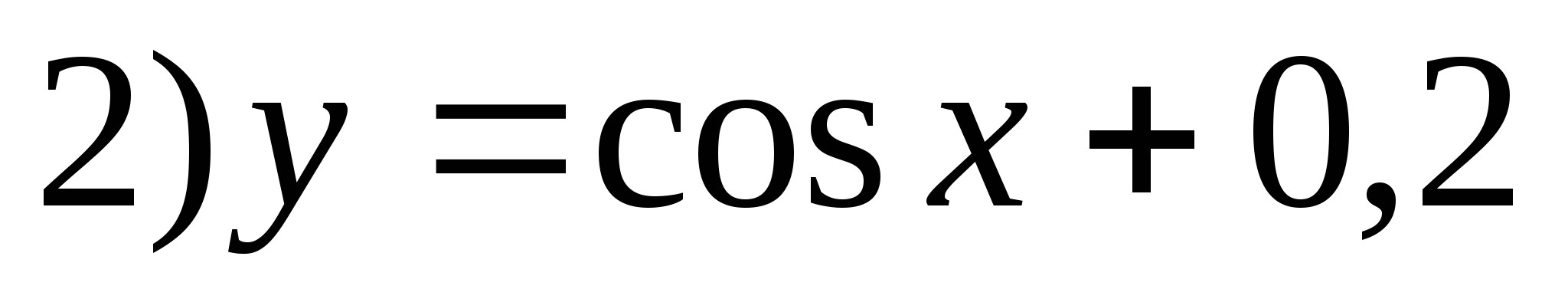
6. Specify the largest negative integer that is not in the range of the function

1) -1 2) -25 3) -6 4) -2

7. How many integers belong to the set of function values

1) 11 2) 3 3) 5 4) 4

Option 5

1. Specify the set of values of the function y = 2 -sin 5 x.

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Find the range of the function

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Specify the smallest integer in the function range

y = 3 + sin 2 2 x.

1) 0 2) 1 3) 3 4) 4

4. Which of the following numbers is included in the set of function values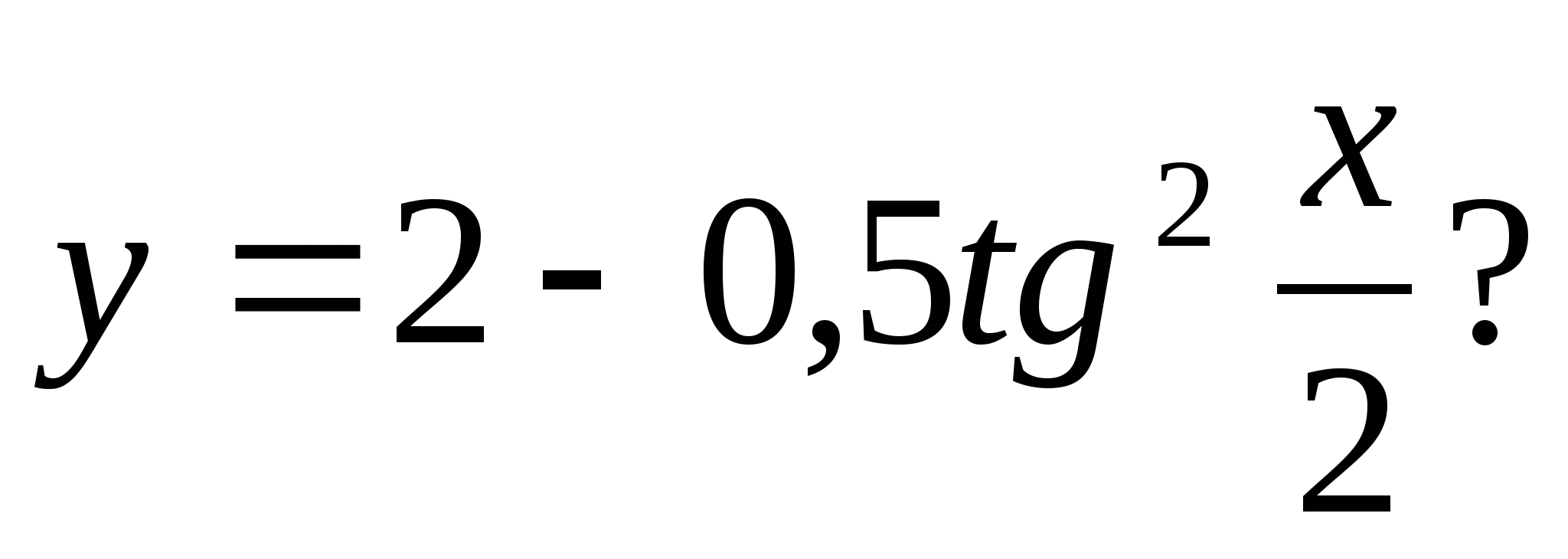

1) 128 2) 10,5 3) 3 4) -235

5. Specify a function whose set of values is the segment [-9;15].

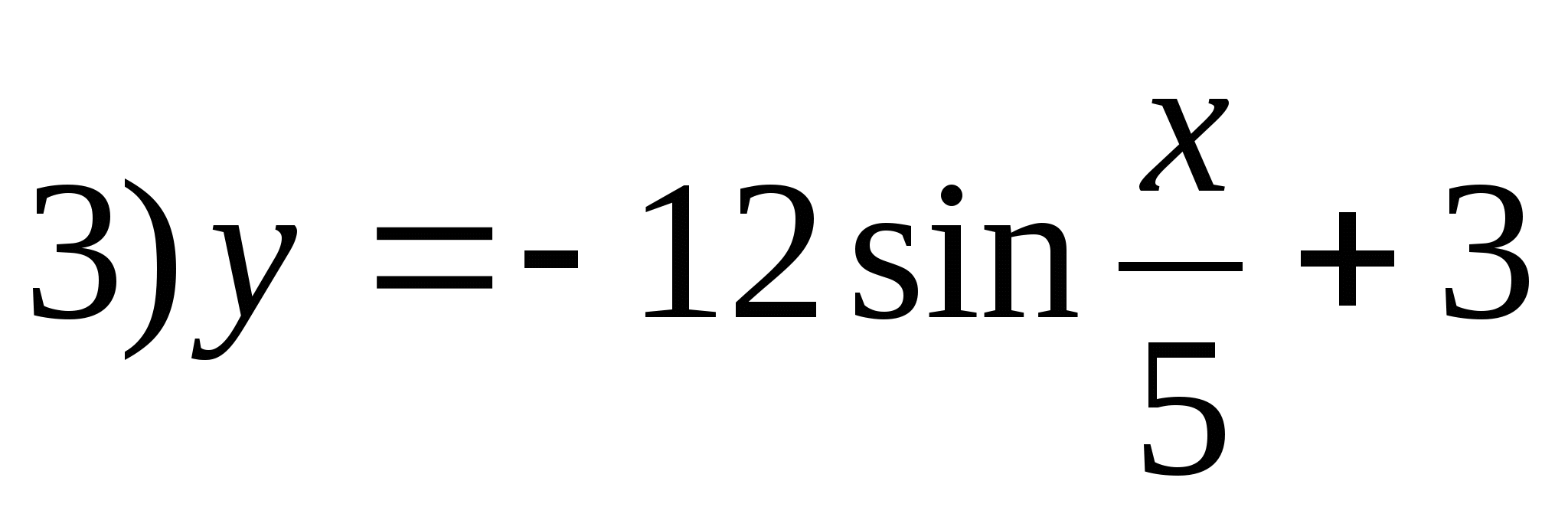
6. Find the sum of integers included in the set of function values

1) 0 2) 7 3) 18 4) 22

7. Find the largest value of the function
on the segment

1) 0,5 2) 1,5 3) 0 4) 2

Option 6

1. Specify the segment corresponding to the set of function values

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Find the range of the function

3. Specify the largest number in the function range

1) 5 2) -6 3) -3 4) 4

4. Which of the following numbers is included in the set of function values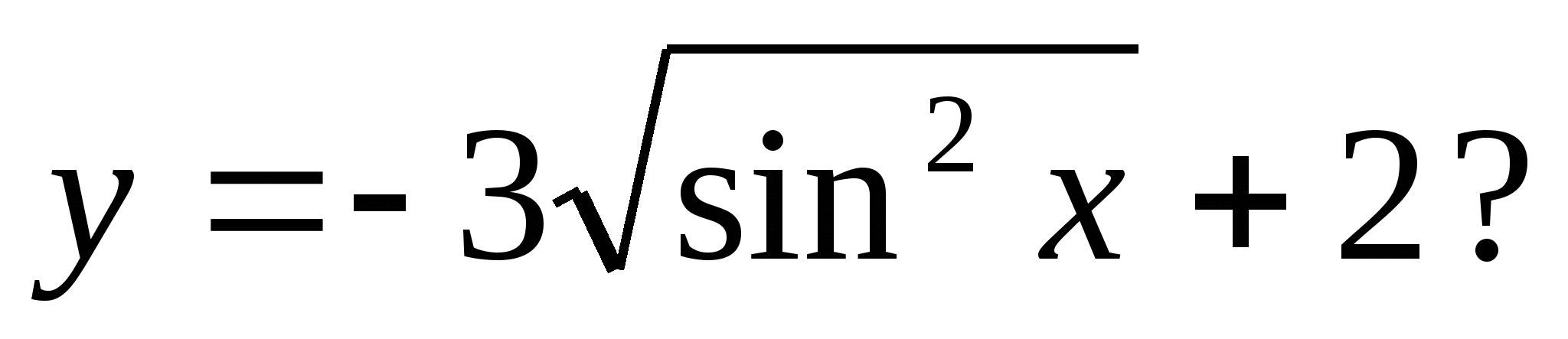

1) 5 2) 0 3) -3 4) 4

5. Specify a function whose set of values is the segment.

1) at = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) y = 5 cos 4 x 4) y = - tg 2 x + 1

6. Find the product of integers included in the set of values

y = 3,8 – 1,4 sin 3 x.

1) 17 2) 12 3) 0 4) 60

7. Find the set of function values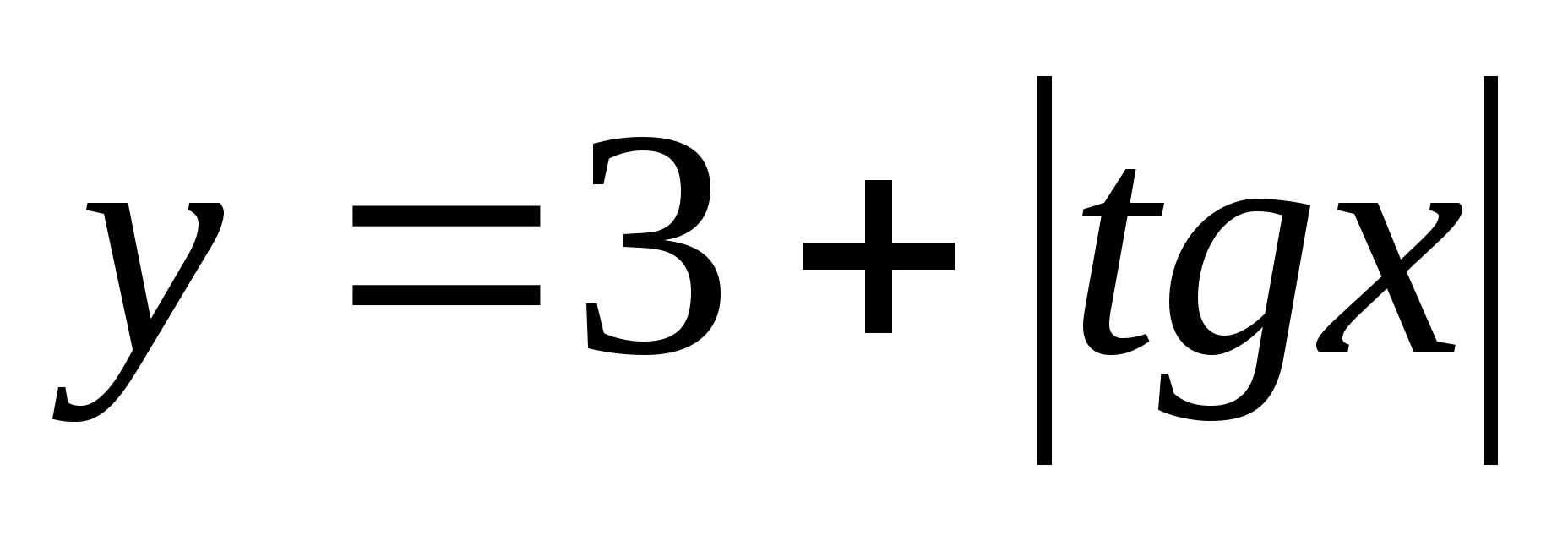
in between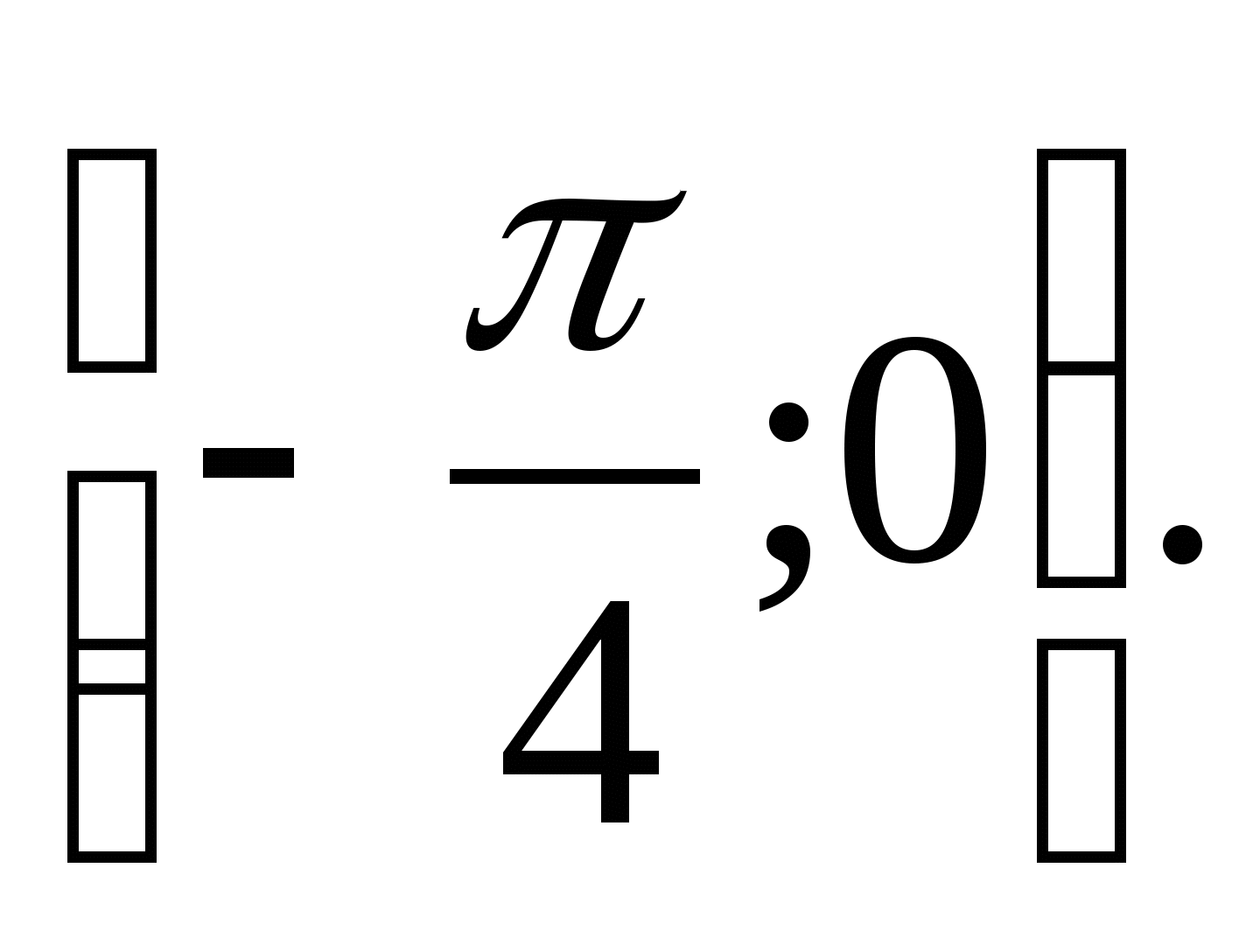

1) (3;4) 2) 3)

Option 7

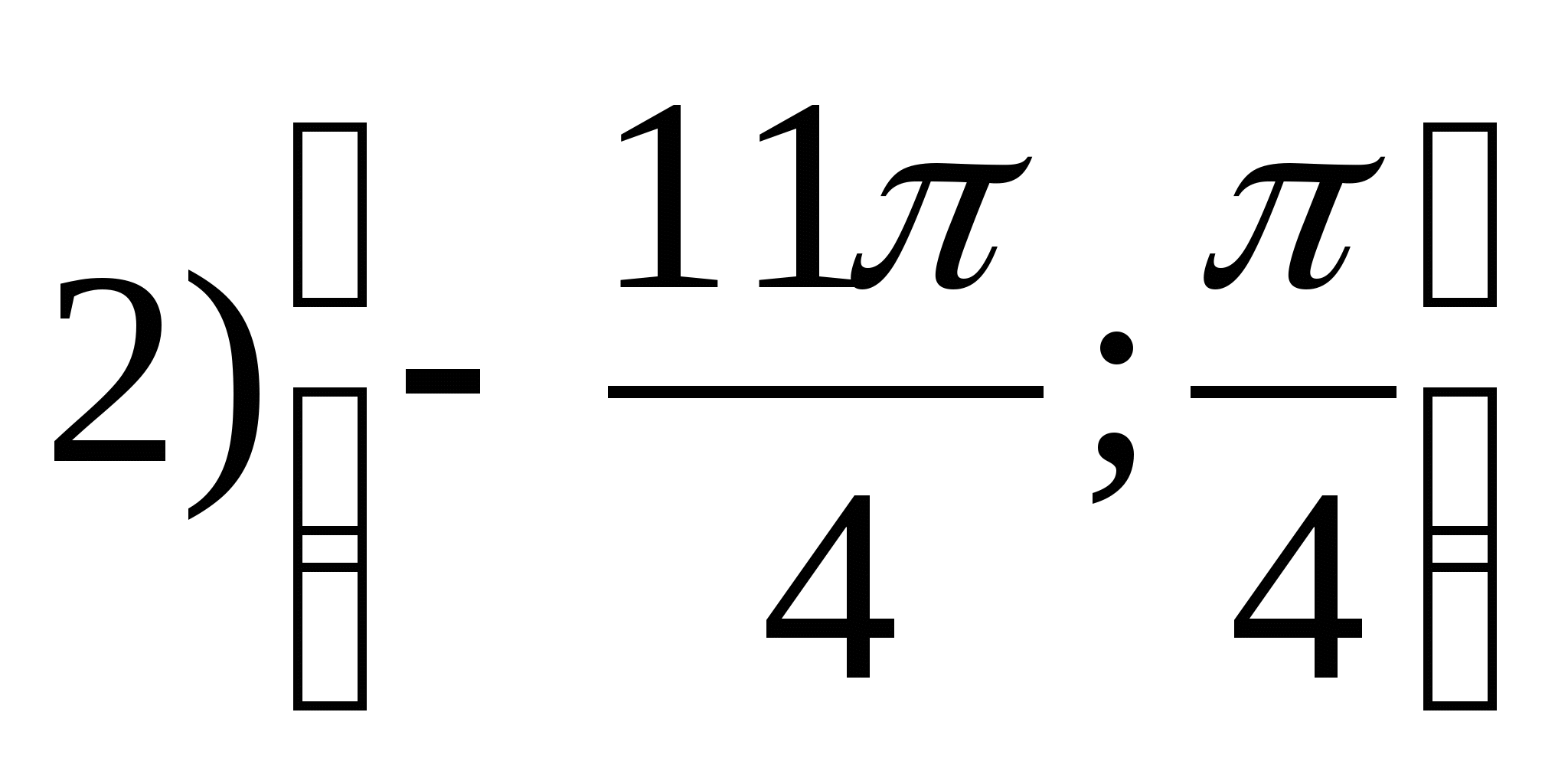
2. Find the smallest integer value of the function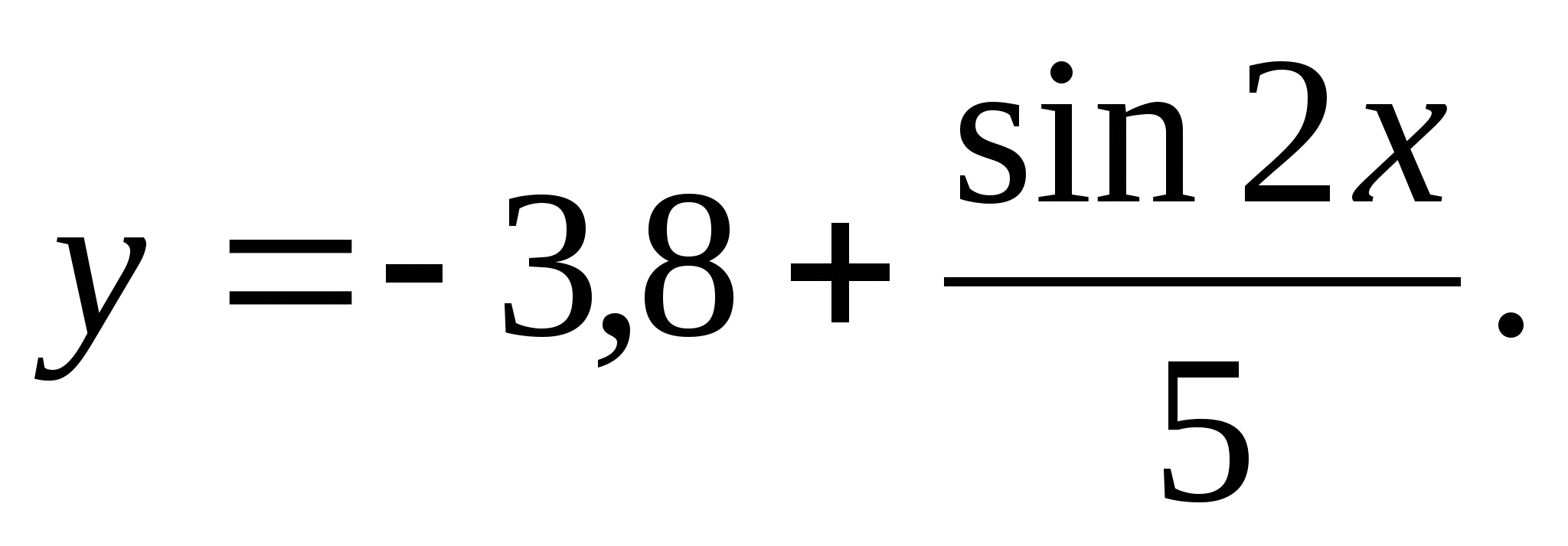

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. For what values of a is the equationsin(3 x-4)+5= a solvable?

1) 2) 3) (4;6) 4) (-6;4]

sin 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

in between

2) 0 3) 1

y = 4 sin(x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Option 8

1. Find the set of function valuesy = arctgx- 2π.

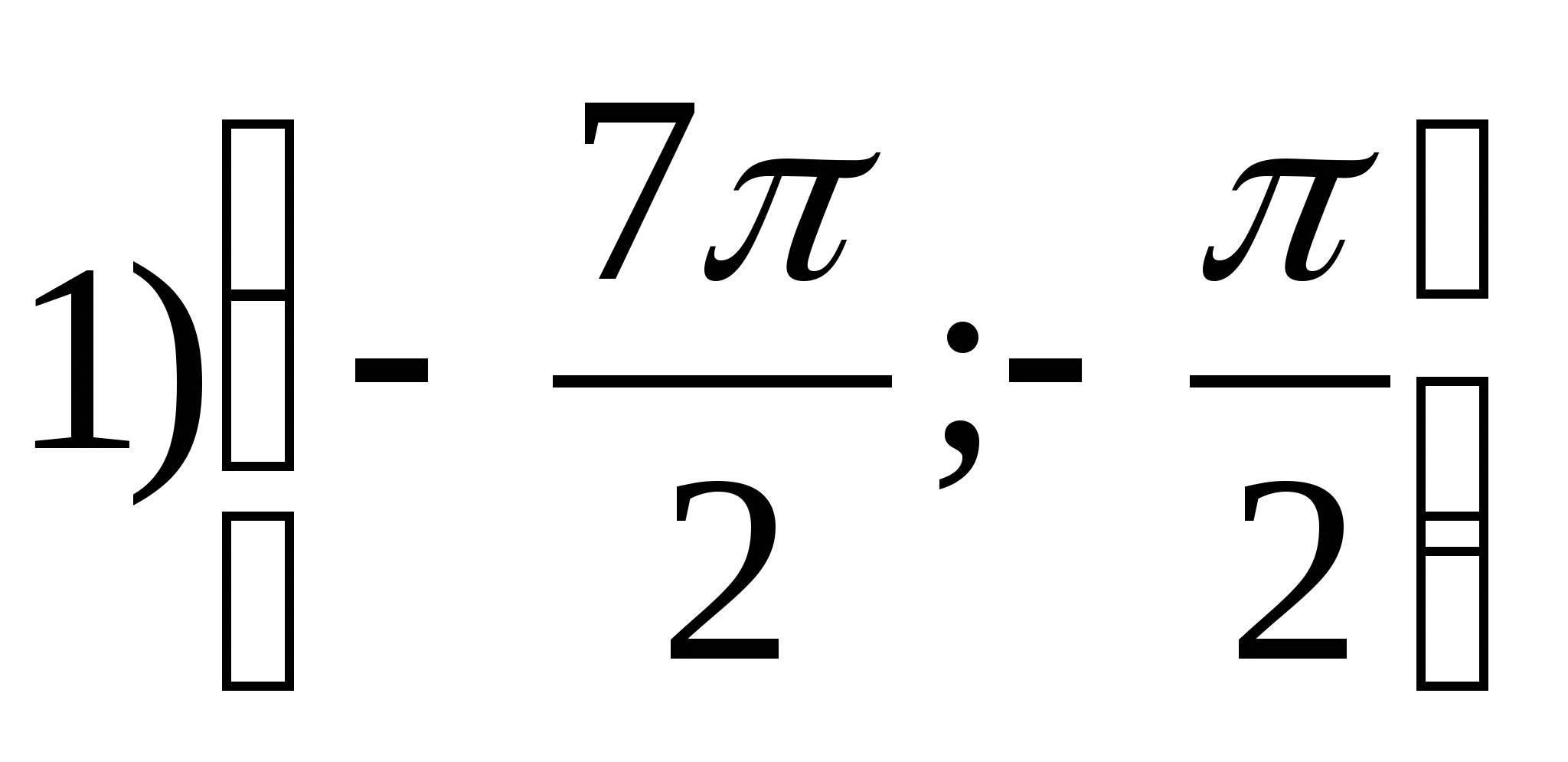
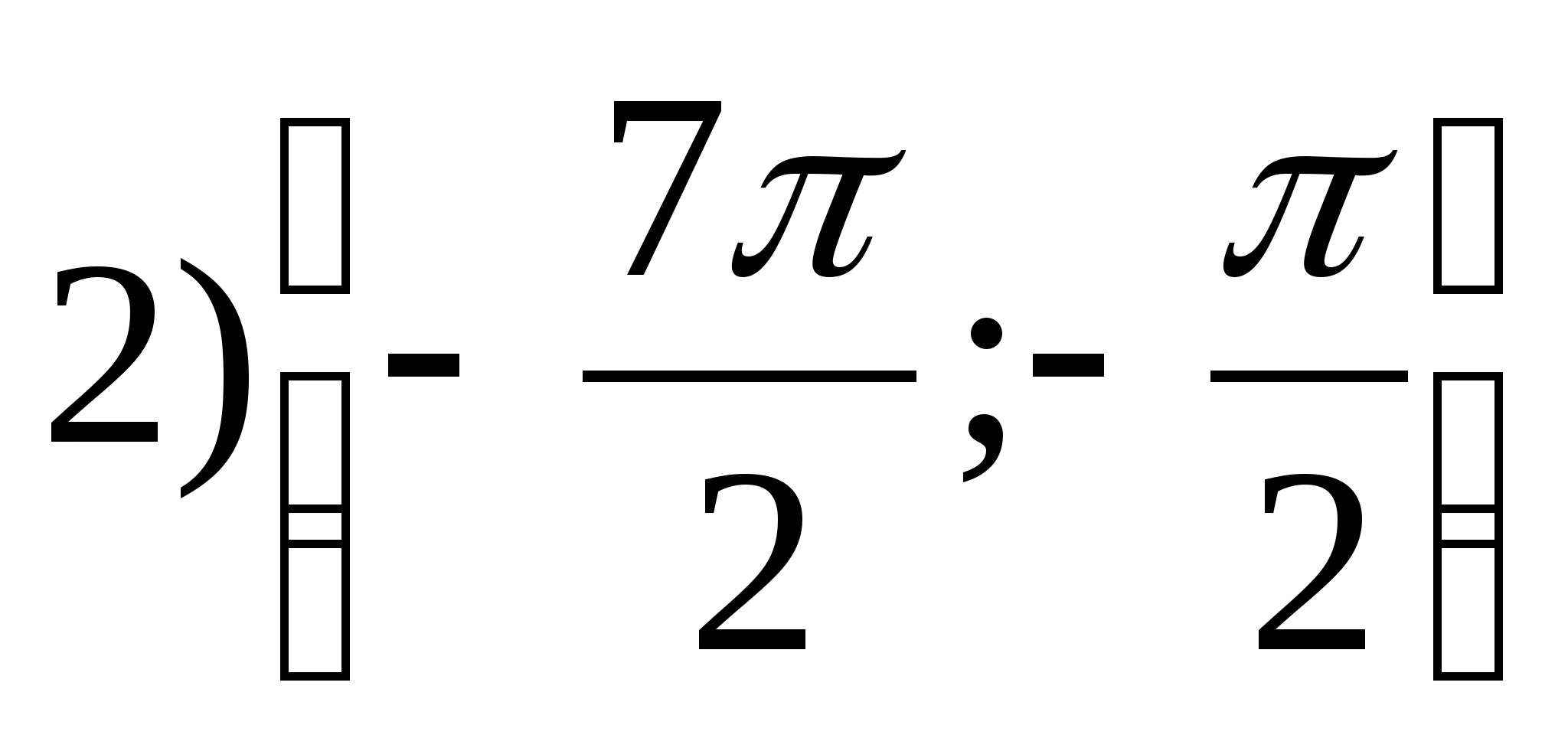
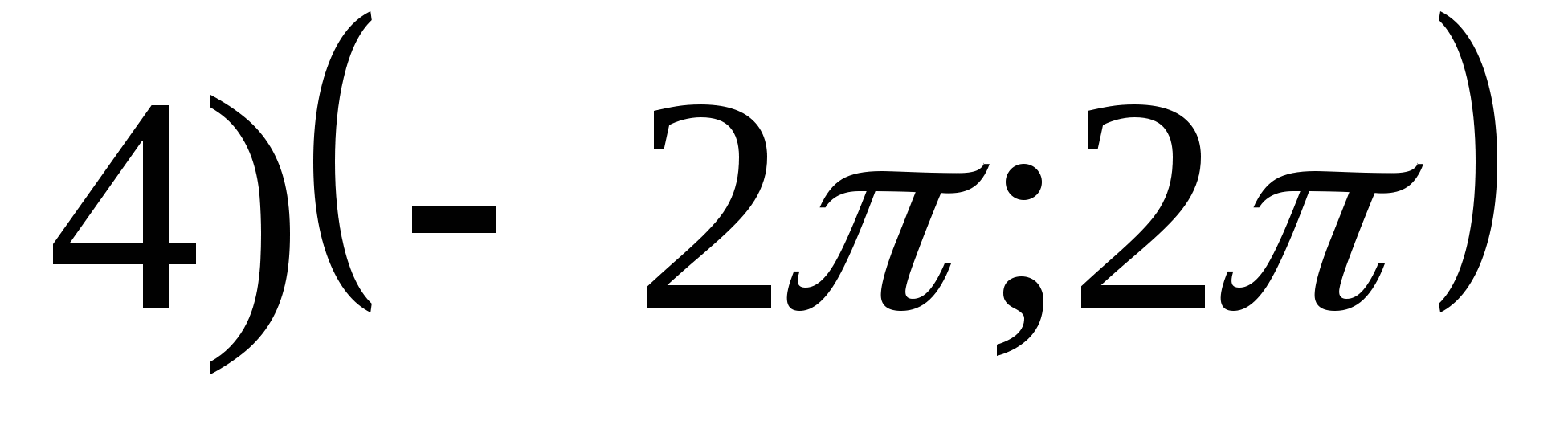
2. Find the largest value of the function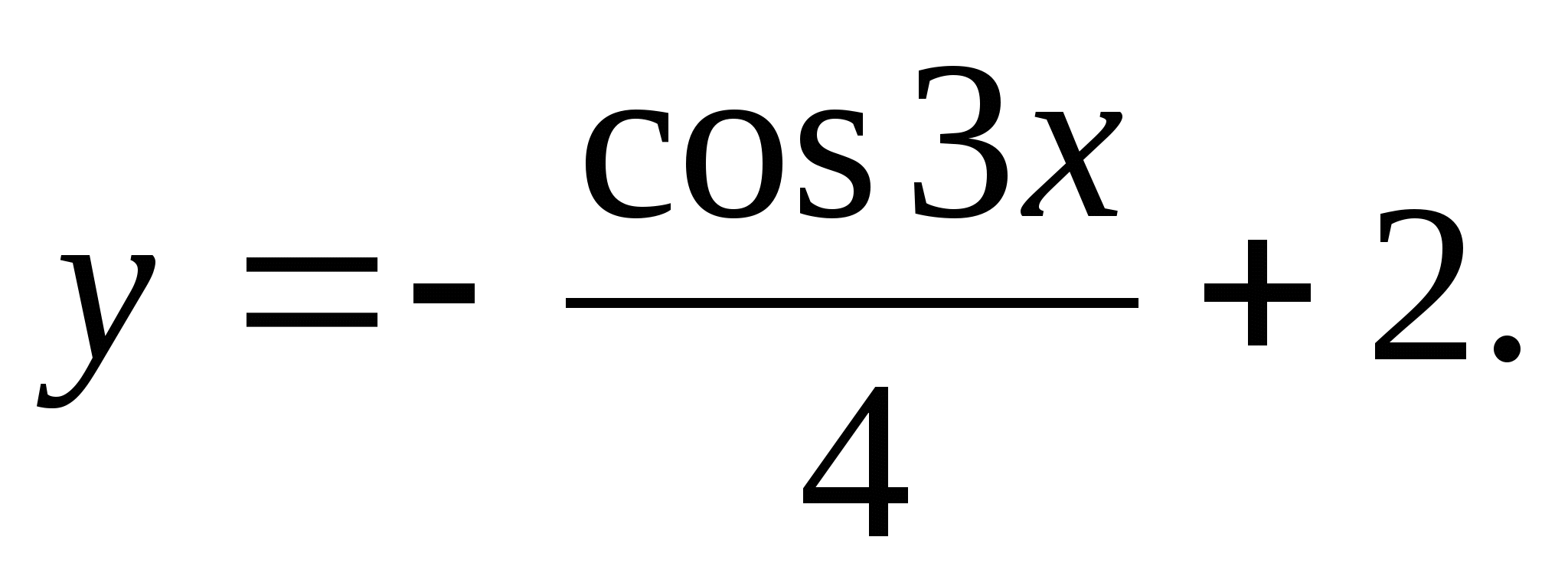

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Which of the following numbers could be the value of the function

1) -4 2) -2 3) 0 4) 2

4. At what values of p does the equation -2+cos(4 x-1)= p has roots?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Find the set of function valuesy = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

in between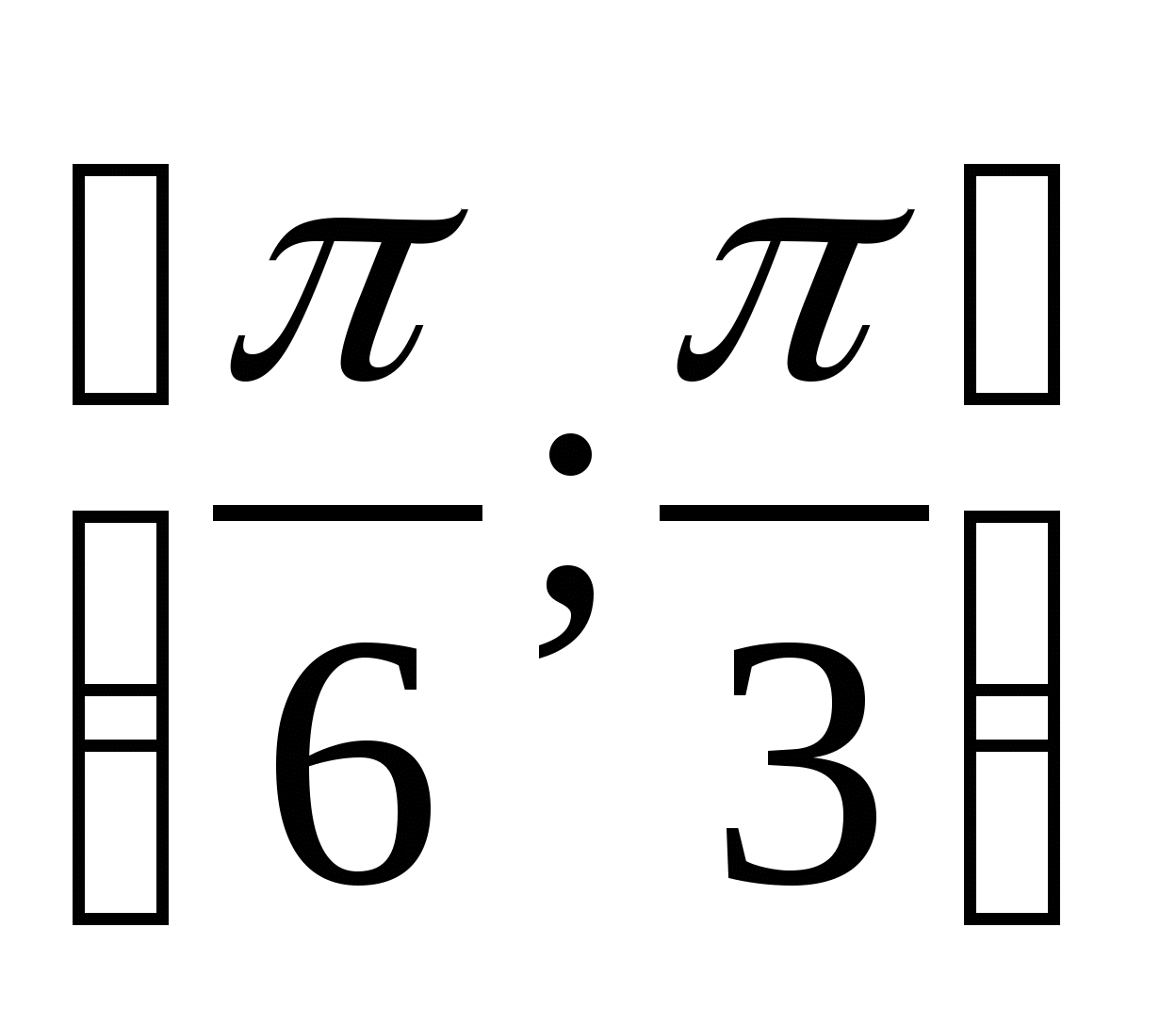
.

1) 0 2) 1 3) -1 4) 3

7. How many integers are in the function range

1) 4 2) 3 3) 5 4) 2

Option 9

1. Find the range of the function

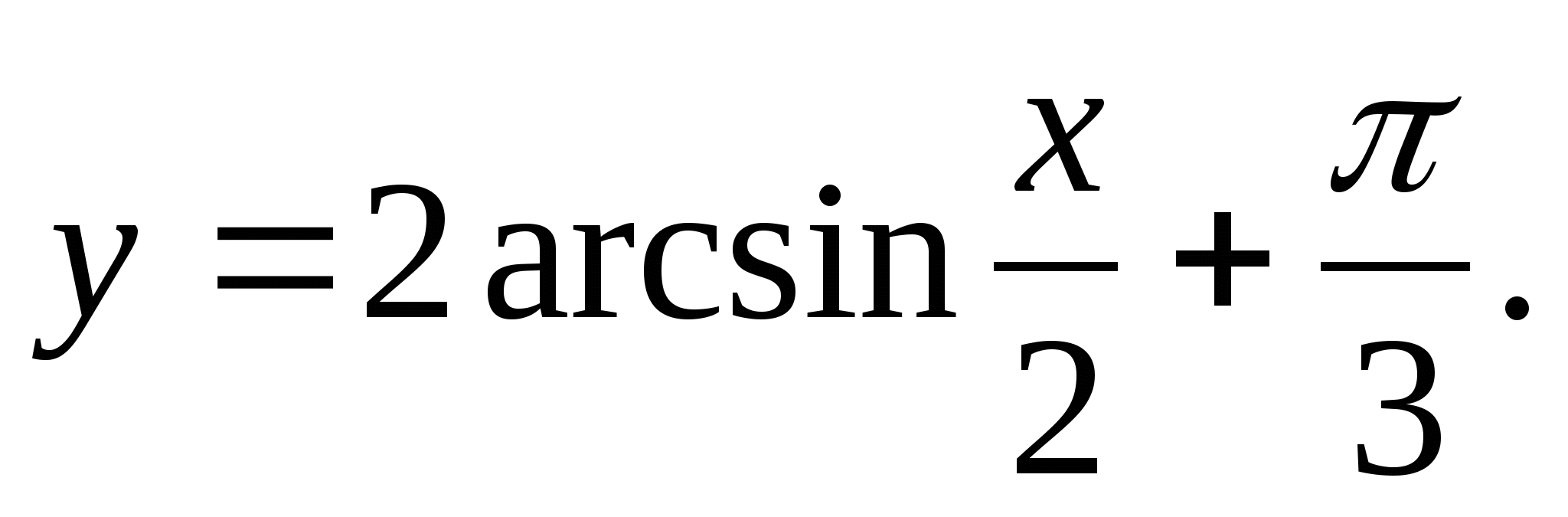
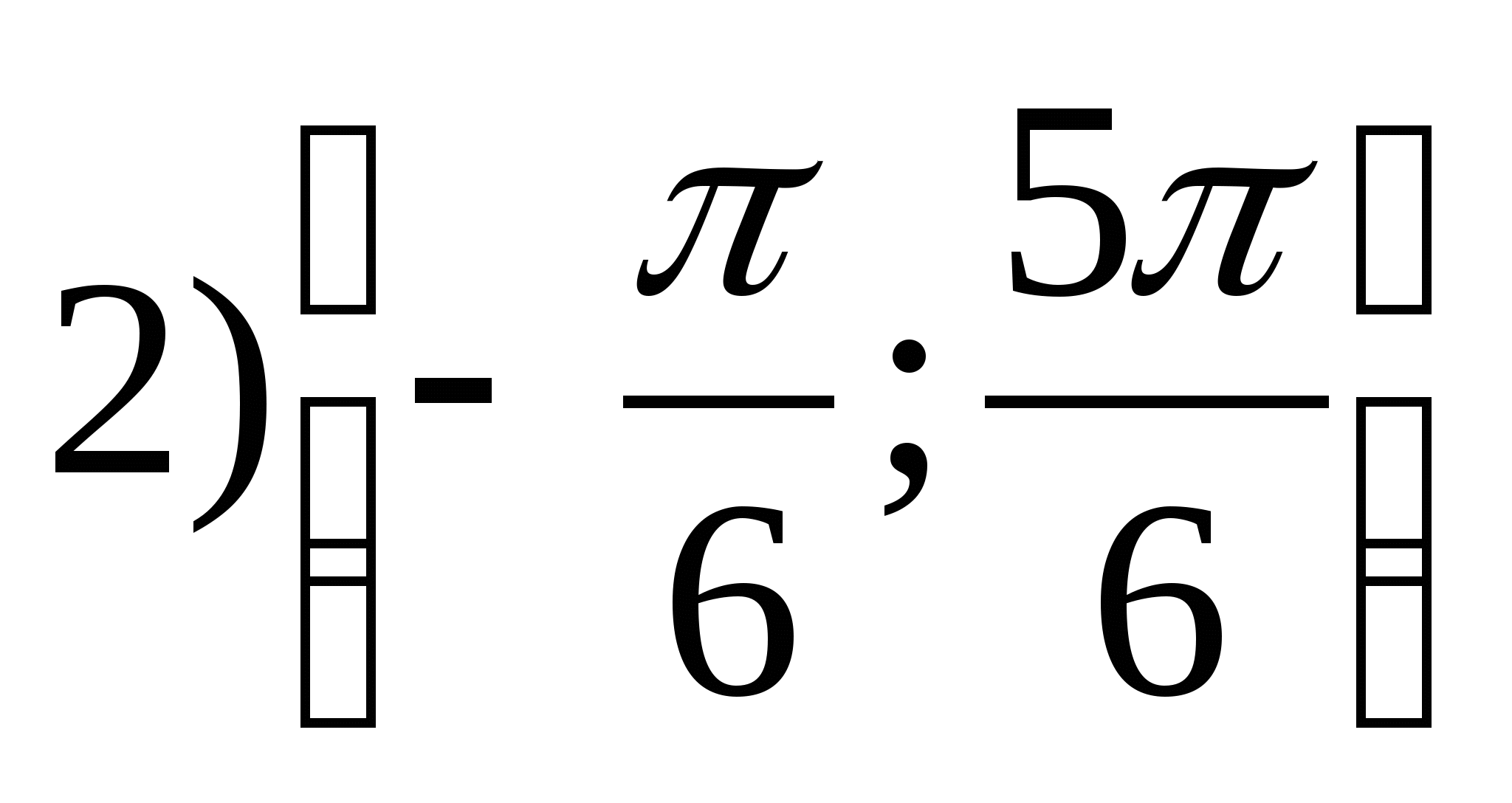
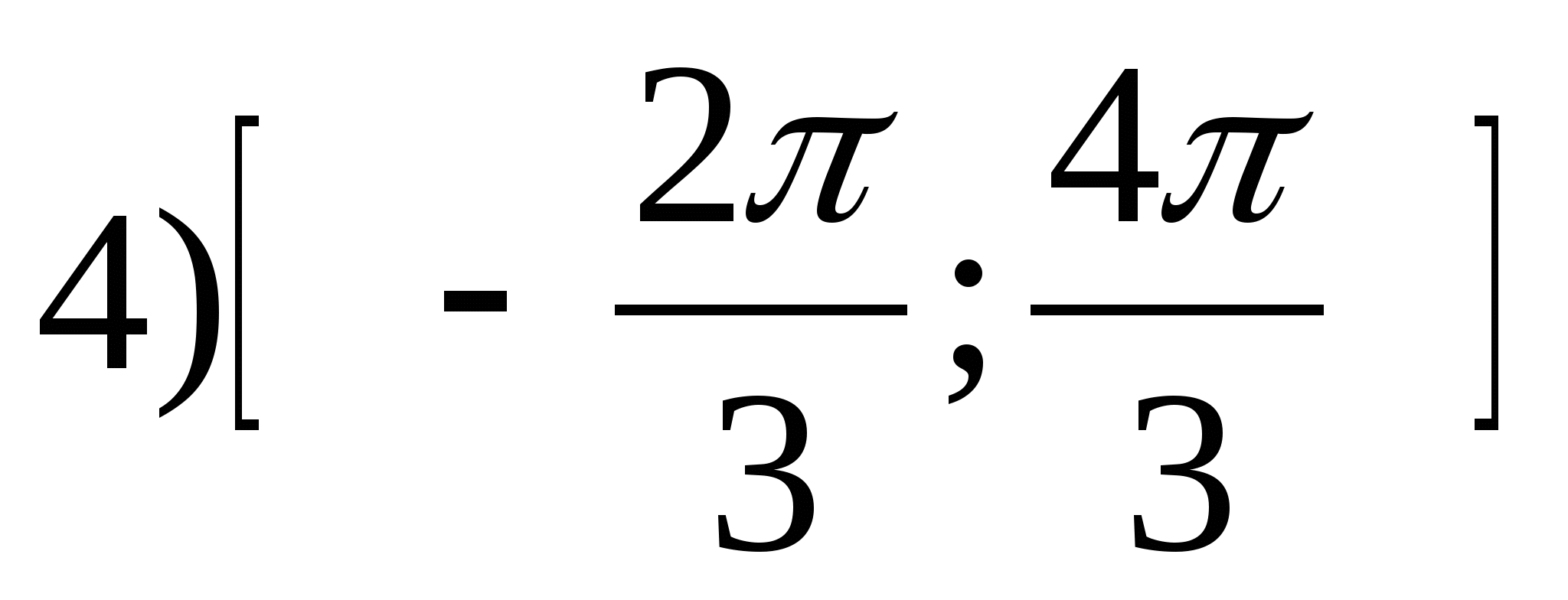
2. Find the largest integer value of the function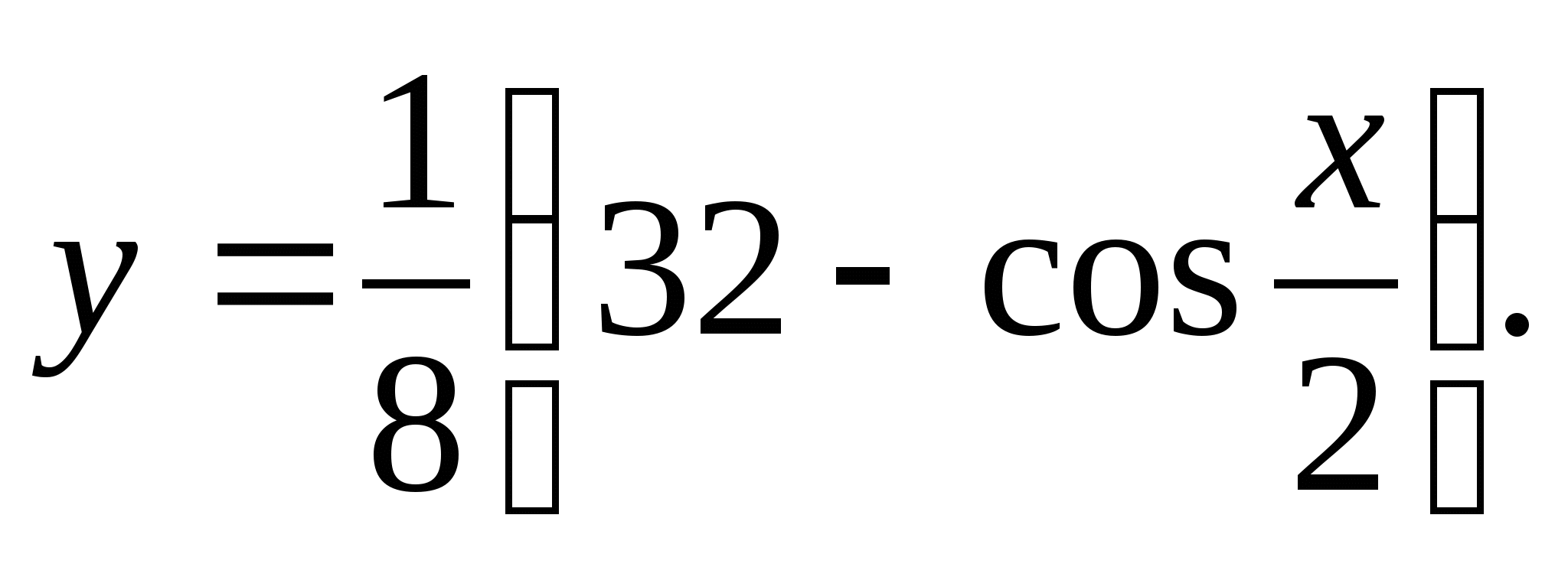

1) 4 2) 5 3) 6 4) 7

3. Which of the following numbers could be the value of the function

1) 0 2) 3 3) 6 4) 9

k the equation - k + sin(2 x-1) = 2 solvable?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Find the set of values of the function y = -cos 2 3 x + 4.

1) 2) 3) 4)

6. Specify the smallest value of the function
in between

2) -1 3) 0 4) 1

7. Find how many integers are included in the range of values of the function y = 12cos 3 x +5 sin 3 x.

1) 13 2) 27 3) 26 4) 14

Option 10

1. Find the range of the function

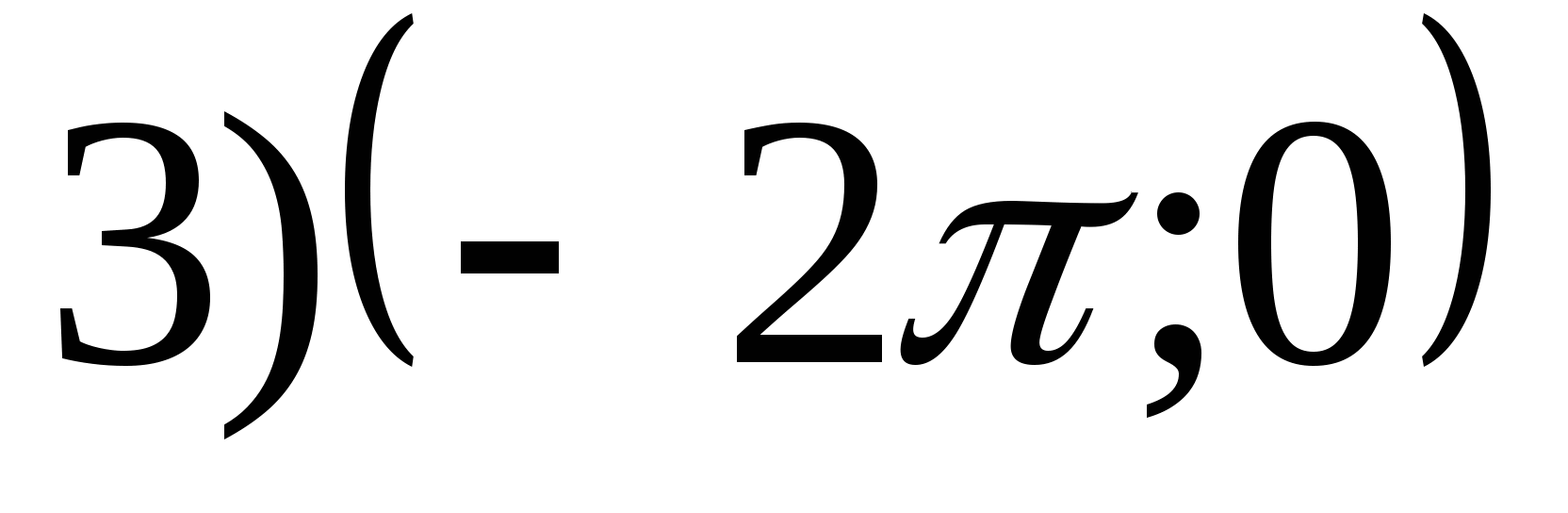
2. Find the smallest value of the function

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Which of the following numbers could be the value of the function

1) -4 2) -1 3) 3 4) 7

4. At what parameter valuesm the equation cos (3 x + 2)- m= 5 has roots?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Find the set of values of the function y = -2ctg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Specify the largest value of the function
in between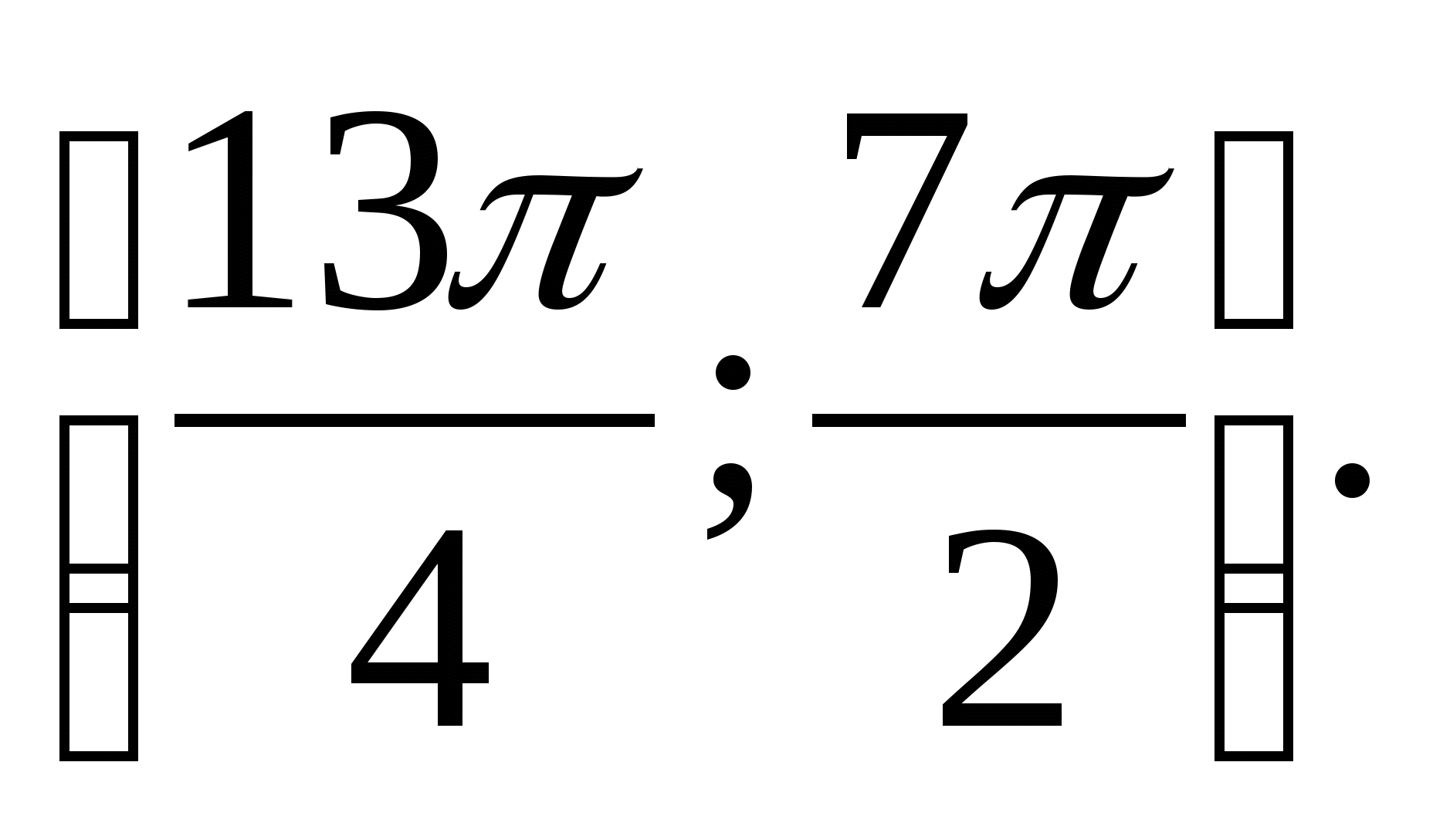

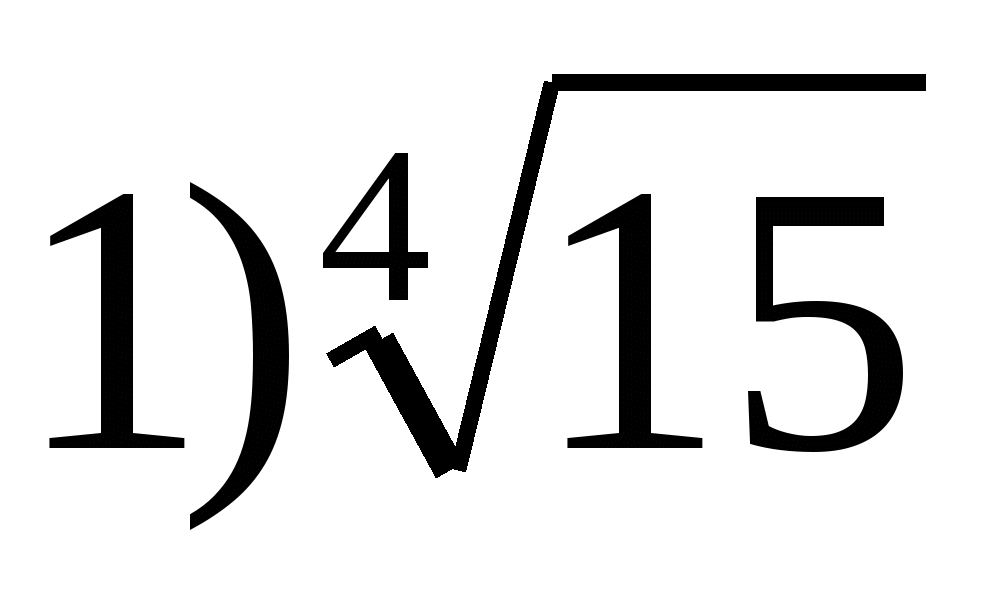2) 0 3) 2 4) 1

7. Find how many integers are in the range of the function

1) 30 2) 35 3) 17 4) 7

Multiple values of exponential and logarithmic functions

Option 1

1. Find the range of the function

1) 4) (-∞;3)

2. Specify multiple function values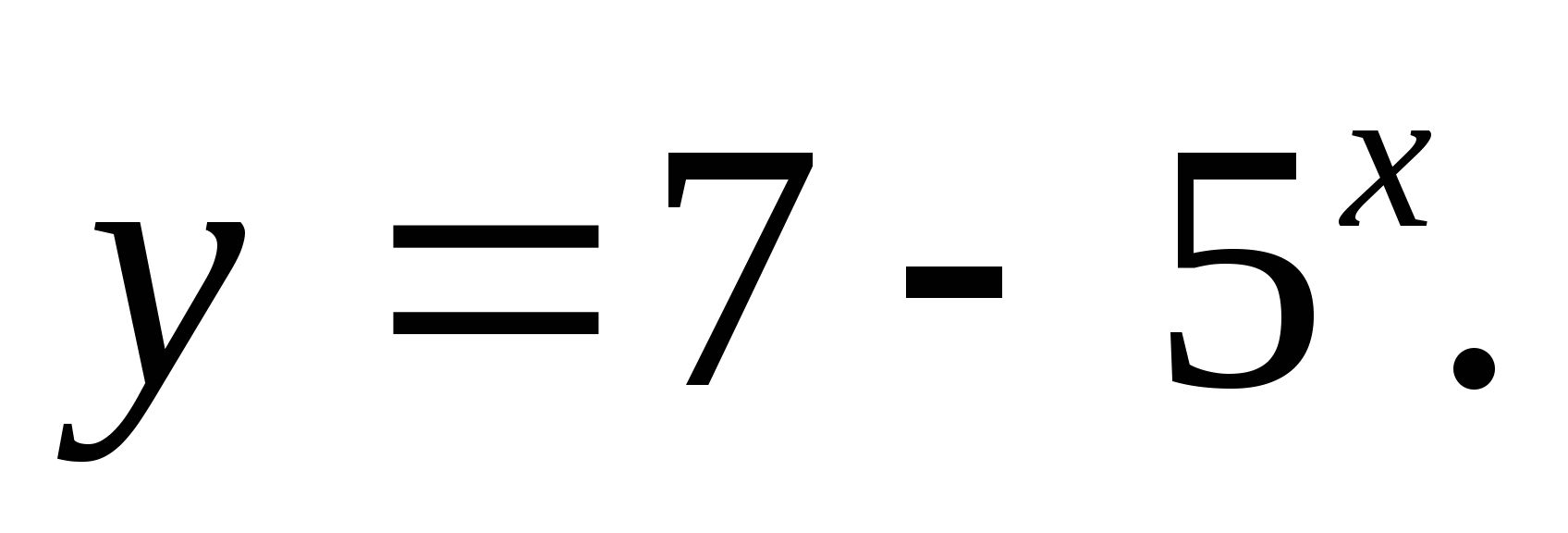

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Specify the smallest integer value of the function

1) 1 2) -1 3) 0 4) -5

7. Specify a function whose set of values is the interval (1;∞).

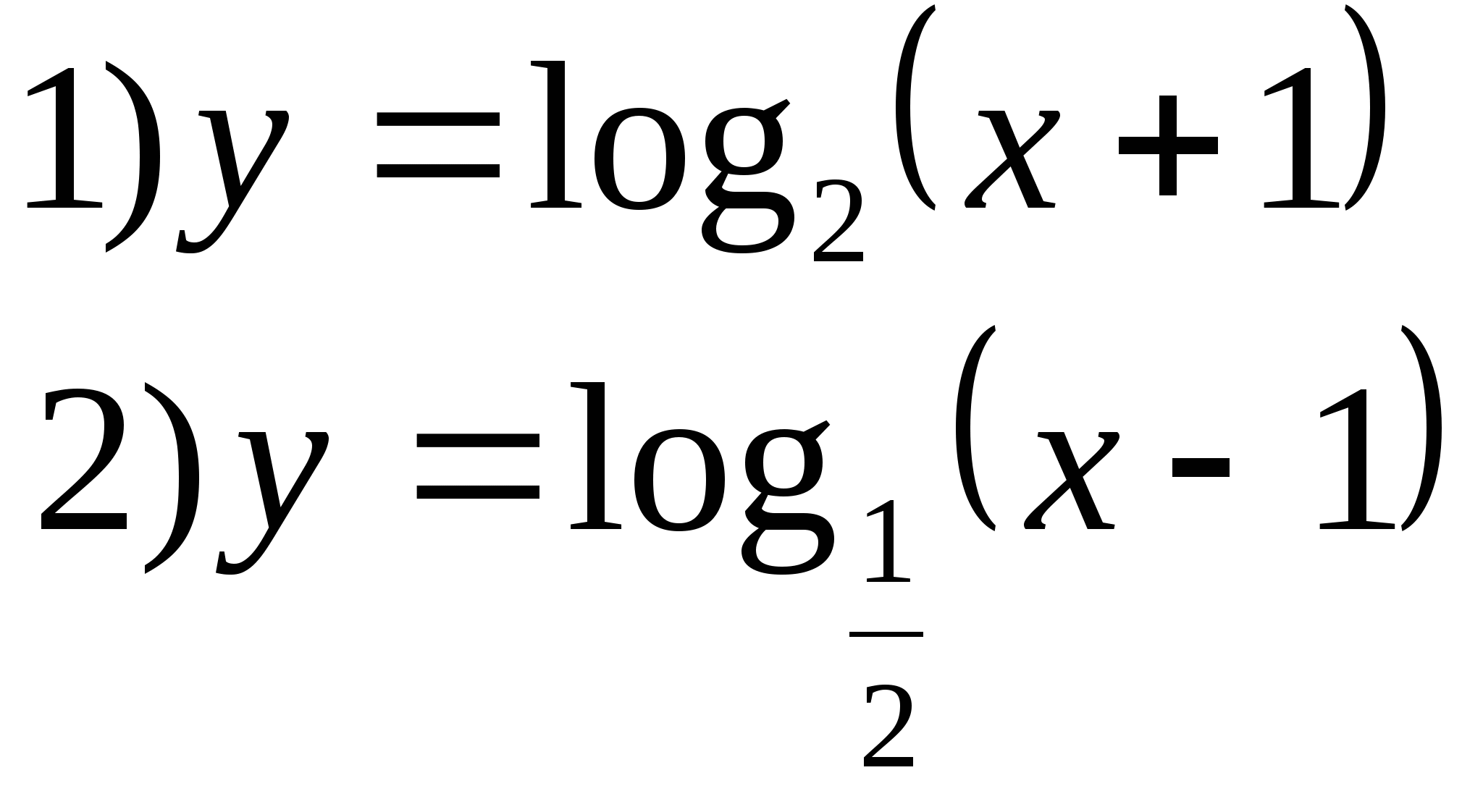
Option 2

1. Specify a set of function values

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Find the range of the function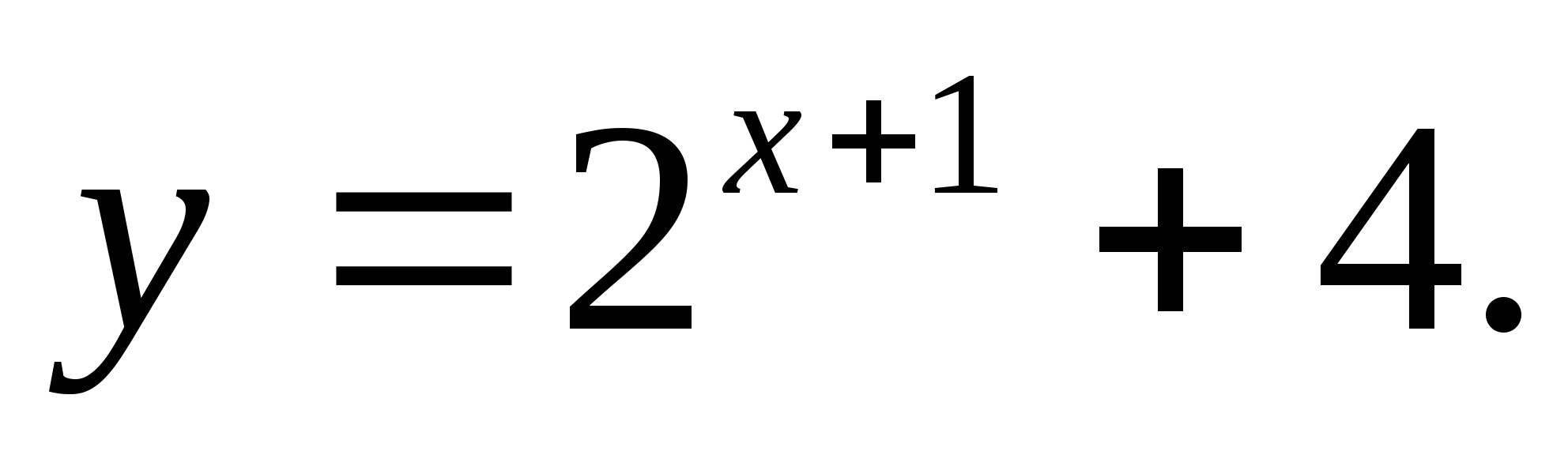

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Specify the smallest integer value of the function

1) -12 2) -11 3) -10 4) -15

4. Specify a number that does not belong to the set of function values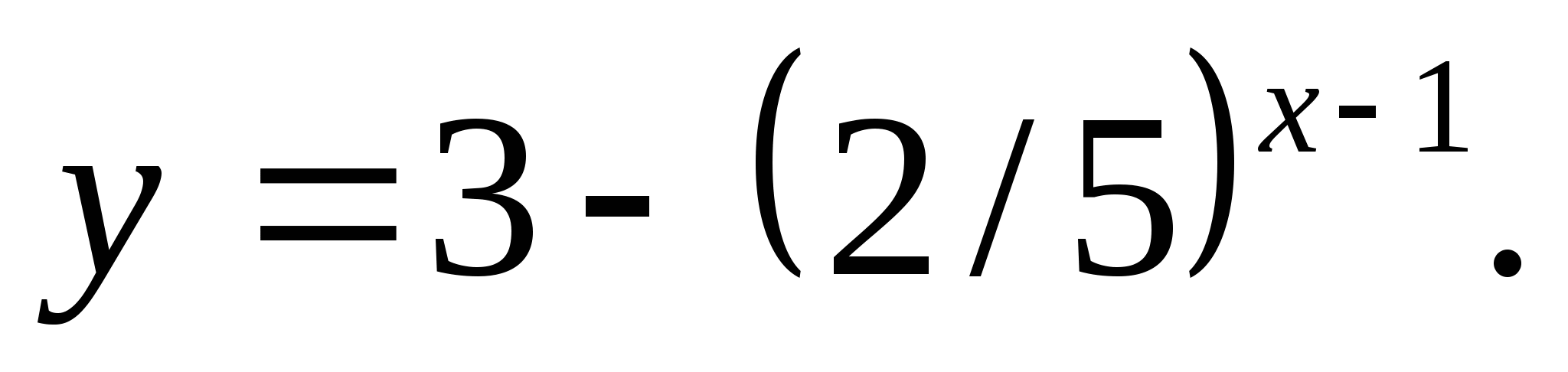

1) -42 2) 3 3) 1 4) -20

5. Specify multiple function values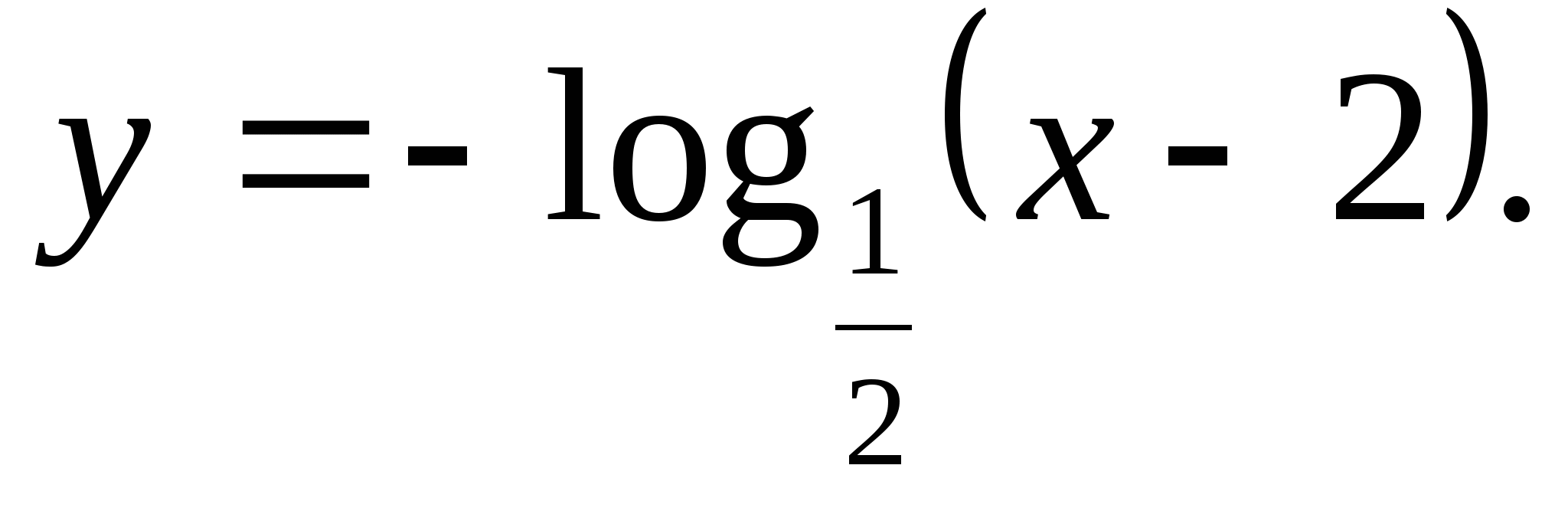

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Specify the largest integer value of the function

1) 10 2) 3 3) 9 4) 2

7. Specify a function whose set of values is the interval

(-∞;13).

Option 5

1. Specify the smallest integer value of the function

1) 0 2) -1 3) -2 4) -3

2. Which of the following numbers is included in the range of the function

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Find on which segment the function
takes the largest value of 2 and the smallest value of -3.

1) 2) (-5;2) 3) 4) (-3;2)

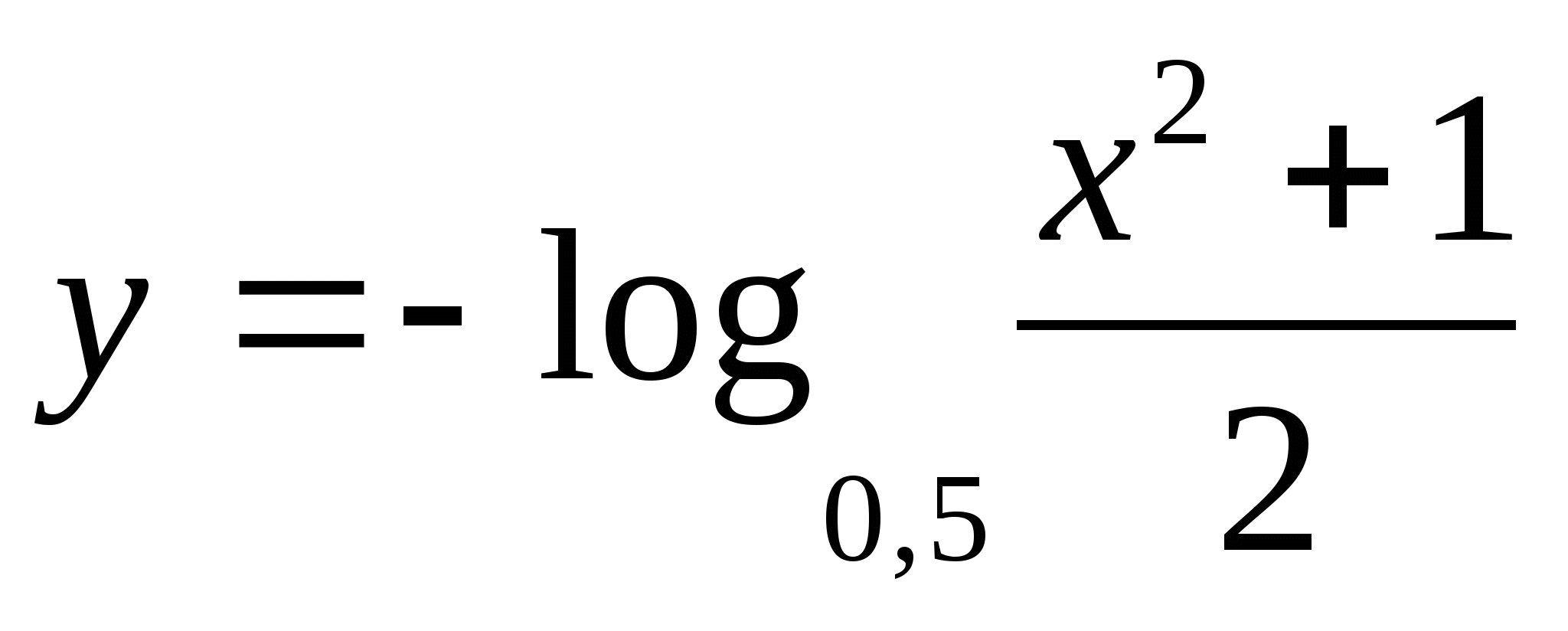in between

1) -1/2 2) 5 3) 2 4) 4

8. Find the sum of all natural numbers not included in the set of function values

1) 3 2) 6 3) 10 4) 8

Option 6

1. Specify the largest integer value of the function

1) 2 2) 4 3) 3 4) 5

2. Which of the following numbers is not included in the range of the function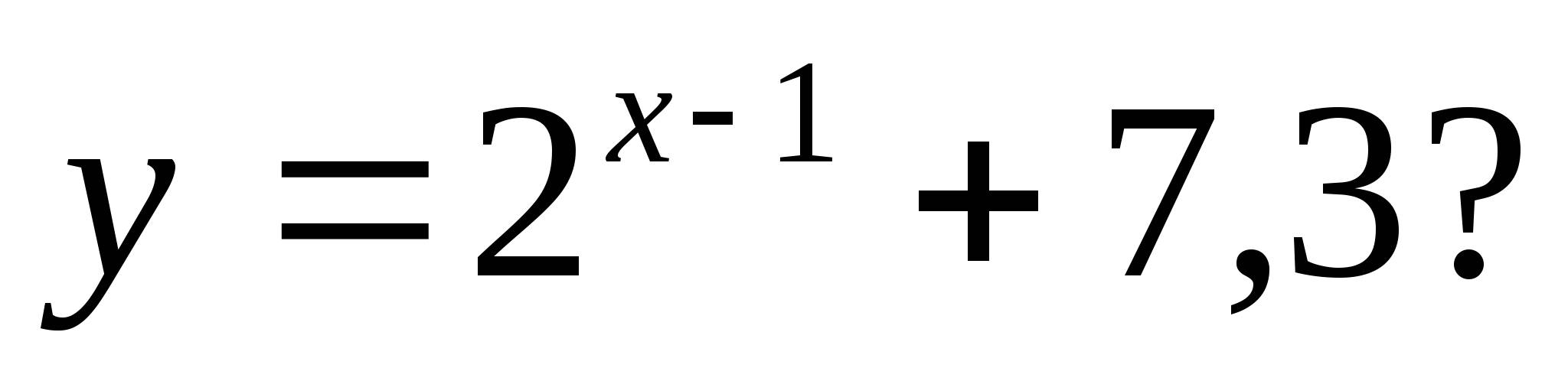

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Specify multiple function values

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Find all points on the op-amp that are projections of points on the graph of the function

1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)

6. Find on which segment the function
takes the smallest value to be -2 and the largest value to be 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Specify the largest value of the function
in between

[-0.9; 0].

2. Find the smallest value of the function on the segment.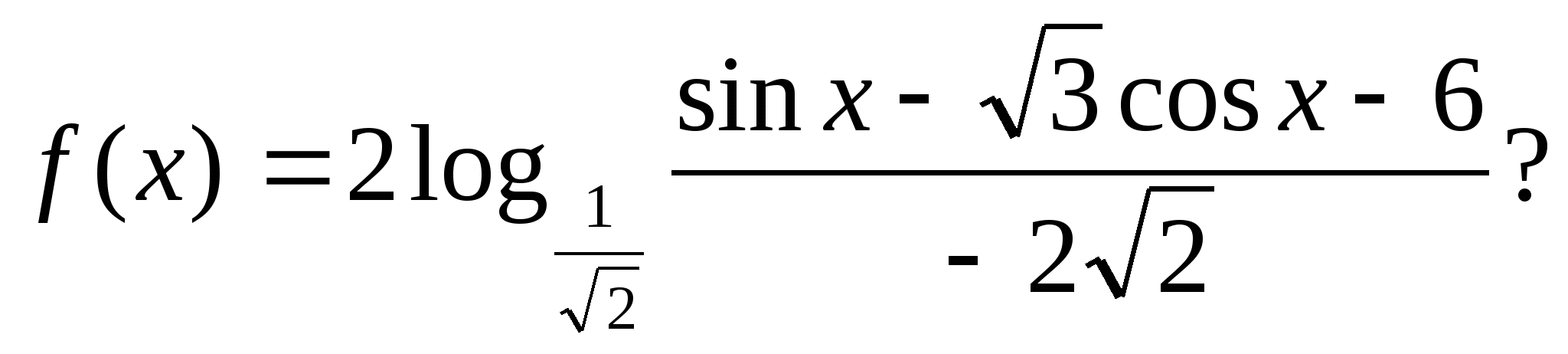

4. How many integer values does the function take?

Answers

Part 1

Multiple values of exponential and logarithmic functions

Part 2

Today in the lesson we will turn to one of the basic concepts of mathematics - the concept of function; Let's take a closer look at one of the properties of a function - the set of its values.

During the classes Teacher.

While solving problems, we notice that sometimes it is finding the set of values of a function that puts us in difficult situations. Why? It would seem that, having studied a function since the 7th grade, we know quite a lot about it. Therefore, we have every reason to make a proactive move. Let’s “play” with many function values ourselves today in order to answer many questions on this topic in the upcoming exam.

During the classes Sets of values of elementary functions

First, you need to repeat the graphs, equations and sets of values of the basic elementary functions throughout the entire domain of definition. Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = R

or one number, for a fractional linear This is our alphabet. By adding to it our knowledge of graph transformations: parallel translation, stretching, compression, reflection, we will be able to solve the problems of the first part

Independent work

U Problem terms and coordinate systems are printed for each student.

1. Find the set of function values over the entire domain of definition:

A) y= 3 sin X ;
b) y = 7 – 2 X ;
V) y= –arccos ( x + 5):
G) y= | arctg x |;
d)

2. Find the set of function values y = x 2 in between J, If:

A) J = ;
b) J = [–1; 5).

3. Define the function analytically (by an equation), if the set of its values is:

1) E(f(x)) = (–∞ ; 2] and f(x) - function

a) quadratic,
b) logarithmic,
c) demonstrative;

2) E(f(x)) = Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = \{7}.

When discussing a task 2independent work, draw students' attention to the fact that, in the case of monotonicity and continuity of the function y=f(x)at a given interval[a;b],its many meanings-interval,whose ends are the values of f(a)and f(b).

Answer options for the task 3.

1.
A) y = –x 2 + 2 , y = –(x + 18) 2 + 2,
y= a(x – x c) 2 + 2 at A < 0.

b) y= –| log 8 x | + 2,

V) y = –| 3 x – 7 | + 2, y = –5 | x | + 3.

2.
a) b)

V) y = 12 – 5x, Where x ≠ 1 .

Finding multiple values of a function using derivative

During the classes In the 10th grade, we became familiar with the algorithm for finding the extrema of a function continuous on a segment and finding its set of values, without relying on the graph of the function. Remember how we did this? ( Using derivative.) Let's remember this algorithm .

1. Make sure the function y = f(x) is defined and continuous on the segment J = [a; b].

2. Find the values of the function at the ends of the segment: f(a) and f(b).

Comment. If we know that the function is continuous and monotonic on J, then you can immediately answer: E(f) = [f(a); f(b)] or E(f) = [f(b); f(A)].

3. Find the derivative and then the critical points x kJ.

4. Find the values of the function at critical points f(x k).

5. Compare function values f(a), f(b) And f(x k), select the largest and smallest values of the function and give the answer: E(f)= [f name; f naib].

Problems involving the use of this algorithm are found in versions of the Unified State Exam. For example, in 2008 such a task was proposed. You have to solve it Houses .

Task C1. Find the largest value of the function

f(x) = (0,5x + 1) 4 – 50(0,5x + 1) 2

at | x + 1| ≤ 3.

Homework conditions are printed for each student .

Finding the set of values of a complex function

During the classes The main part of our lesson will be non-standard problems containing complex functions, the derivatives of which are very complex expressions. And the graphs of these functions are unknown to us. Therefore, to solve, we will use the definition of a complex function, that is, the dependence between variables in the order of their nesting in a given function, and an assessment of their range of values (the interval of change in their values). Problems of this type are found in the second part of the Unified State Exam. Let's look at some examples.

Exercise 1. For functions y = f(x) And y = g(x) write a complex function y = f(g(x)) and find its set of values:

A) f(x) = –x 2 + 2x + 3, g(x) = sin x;
b) f(x) = –x 2 + 2x + 3, g(x) = log 7 x;
V) g(x) = x 2 + 1;
G)

Solution. a) The complex function has the form: y= –sin 2 x+ 2sin x + 3.

Introducing an intermediate argument t, we can write this function like this:

y= –t 2 + 2t+ 3, where t= sin x.

At the internal function t= sin x the argument accepts any values, and the set of its values is the segment [–1; 1].

Thus, for the outer function y = –t 2 +2t+ 3 we found out the interval for changing the values of its argument t: t[-1; 1]. Let's look at the graph of the function y = –t 2 +2t + 3.

We note that the quadratic function at t[-1; 1] takes the smallest and largest values at its ends: y name = y(–1) = 0 and y naib = y(1) = 4. And since this function is continuous on the interval [–1; 1], then it accepts all values between them.

Answer: y .

b) The composition of these functions leads us to a complex function which, after introducing an intermediate argument, can be represented as follows:

y= –t 2 + 2t+ 3, where t= log 7 x,

Function t= log 7 x

x (0; +∞ ), t (–∞ ; +∞ ).

Function y = –t 2 + 2t+ 3 (see graph) argument t takes any values, and the quadratic function itself takes all values no more than 4.

Answer: y (–∞ ; 4].

c) The complex function has the following form:

Introducing an intermediate argument, we get:

Where t = x 2 + 1.

Since for the inner function x Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = , A t .

Answer: y (0; 3].

d) The composition of these two functions gives us a complex function

which can be written as

notice, that

So, when

Where k Z , t [–1; 0) (0; 1].

By drawing a graph of the function we see that with these values t

y(–∞ ; –4] c ;

b) throughout the entire definition area.

Solution. First, we examine this function for monotonicity. Function t= arcctg x- continuous and decreasing by Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = and the set of its values (0; π). Function y= log 5 t is defined on the interval (0; π), is continuous and increases on it. This means that this complex function decreases on the set Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = . And it, as a composition of two continuous functions, will be continuous on Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = .

Let's solve problem "a".

Since the function is continuous on the entire number line, it is continuous on any part of it, in particular, on a given segment. And then on this segment it has the smallest and largest values and takes all values between them:

f(4) = log 5 arcctg 4.

Which of the resulting values is greater? Why? And what will be the set of values?

Answer:

Let's solve problem "b".

Answer: at(–∞ ; log 5 π) over the entire definition area.

Problem with a parameter

Now let's try to create and solve a simple equation with a parameter of the form f(x) = a, Where f(x) - the same function as in task 4.

Task 5. Determine the number of roots of the equation log 5 (arcctg x) = A for each parameter value A.

Solution. As we have already shown in task 4, the function at= log 5(arcctg x) - decreases and is continuous on Graphs of functions are projected onto the screen: linear, quadratic, fractional-rational, trigonometric, exponential and logarithmic, for each of them a set of values is verbally determined. Draw students' attention to the fact that the linear function E(f) = and takes values less than log 5 π. This information is enough to give an answer.

Answer: If A < log 5 π, то уравнение имеет единственный корень;

If A≥ log 5 π, then there are no roots.

During the classes Today we looked at problems related to finding the set of values of a function. Along this path, we discovered a new method for solving equations and inequalities - the estimation method, so finding the set of values of a function became a means of solving higher-level problems. In doing so, we saw how such problems are constructed and how the properties of the monotonicity of a function facilitate their solution.

And I would like to hope that the logic that connected the tasks discussed today amazed or at least surprised you. It cannot be otherwise: climbing to a new peak leaves no one indifferent! We notice and appreciate beautiful paintings, sculptures, etc. But mathematics also has its own beauty, attractive and bewitching - the beauty of logic. Mathematicians say that a beautiful solution is usually a correct solution, and this is not just a phrase. Now you have to find such solutions yourself, and we have indicated one of the paths to them today. Good luck to you! And remember: the one who walks will master the road!

Many problems lead us to search for a set of function values on a certain segment or throughout the entire domain of definition. Such tasks include various evaluations of expressions and solving inequalities.

In this article, we will define the range of values of a function, consider methods for finding it, and analyze in detail the solution of examples from simple to more complex. All material will be provided with graphic illustrations for clarity. So this article is a detailed answer to the question of how to find the range of a function.

Definition.

The set of values of the function y = f(x) on the interval X is the set of all values of a function that it takes when iterating over all .

Definition.

Function range y = f(x) is the set of all values of a function that it takes when iterating over all x from the domain of definition.

The range of the function is denoted as E(f) .

The range of a function and the set of values of a function are not the same thing. We will consider these concepts equivalent if the interval X when finding the set of values of the function y = f(x) coincides with the domain of definition of the function.

Also, do not confuse the range of the function with the variable x for the expression on the right side of the equality y=f(x) . The range of permissible values of the variable x for the expression f(x) is the domain of definition of the function y=f(x) .

The figure shows several examples.

Graphs of functions are shown with thick blue lines, thin red lines are asymptotes, red dots and lines on the Oy axis show the range of values of the corresponding function.

As you can see, the range of values of a function is obtained by projecting the graph of the function onto the y-axis. It can be one single number (first case), a set of numbers (second case), a segment (third case), an interval (fourth case), an open ray (fifth case), a union (sixth case), etc.

So what do you need to do to find the range of values of a function?

Let's start with the simplest case: we will show how to determine the set of values of a continuous function y = f(x) on the segment.

It is known that a function continuous on an interval reaches its maximum and minimum values on it. Thus, the set of values of the original function on the segment will be the segment . Consequently, our task comes down to finding the largest and smallest values of the function on the segment.

For example, let's find the range of values of the arcsine function.

Example.

Specify the range of the function y = arcsinx .

Solution.

The area of definition of the arcsine is the segment [-1; 1] . Let's find the largest and smallest value of the function on this segment.

The derivative is positive for all x from the interval (-1; 1), that is, the arcsine function increases over the entire domain of definition. Consequently, it takes the smallest value at x = -1, and the largest at x = 1.

We have obtained the arcsine function range .

Example.

Find the set of function values on the segment.

Solution.

Let's find the largest and smallest value of the function on a given segment.

Let us determine the extremum points belonging to the segment:

We calculate the values of the original function at the ends of the segment and at points :

Therefore, the set of values of a function on an interval is the interval .

Now we will show how to find the set of values of a continuous function y = f(x) in the intervals (a; b) , .

First, we determine the extremum points, extrema of the function, intervals of increase and decrease of the function on a given interval. Next, we calculate at the ends of the interval and (or) the limits at infinity (that is, we study the behavior of the function at the boundaries of the interval or at infinity). This information is enough to find the set of function values on such intervals.

Example.

Define the set of function values on the interval (-2; 2) .

Solution.

Let's find the extremum points of the function falling on the interval (-2; 2):

Dot x = 0 is a maximum point, since the derivative changes sign from plus to minus when passing through it, and the graph of the function goes from increasing to decreasing.

there is a corresponding maximum of the function.

Let's find out the behavior of the function as x tends to -2 on the right and as x tends to 2 on the left, that is, we find one-sided limits:

What we got: when the argument changes from -2 to zero, the function values increase from minus infinity to minus one-fourth (the maximum of the function at x = 0), when the argument changes from zero to 2, the function values decrease to minus infinity. Thus, the set of function values on the interval (-2; 2) is .

Example.

Specify the set of values of the tangent function y = tgx on the interval.

Solution.

The derivative of the tangent function on the interval is positive , which indicates an increase in function. Let's study the behavior of the function at the boundaries of the interval:

Thus, when the argument changes from to, the function values increase from minus infinity to plus infinity, that is, the set of tangent values on this interval is the set of all real numbers.

Example.

Find the range of the natural logarithm function y = lnx.

Solution.

The natural logarithm function is defined for positive values of the argument . On this interval the derivative is positive , this indicates an increase in the function on it. Let's find the one-sided limit of the function as the argument tends to zero on the right, and the limit as x tends to plus infinity:

We see that as x changes from zero to plus infinity, the values of the function increase from minus infinity to plus infinity. Therefore, the range of the natural logarithm function is the entire set of real numbers.

Example.

Solution.

This function is defined for all real values of x. Let us determine the extremum points, as well as the intervals of increase and decrease of the function.

Consequently, the function decreases at , increases at , x = 0 is the maximum point, the corresponding maximum of the function.

Let's look at the behavior of the function at infinity:

Thus, at infinity the values of the function asymptotically approach zero.

We found out that when the argument changes from minus infinity to zero (the maximum point), the function values increase from zero to nine (to the maximum of the function), and when x changes from zero to plus infinity, the function values decrease from nine to zero.

Look at the schematic drawing.

Now it is clearly visible that the range of values of the function is .

Finding the set of values of the function y = f(x) on intervals requires similar research. We will not dwell on these cases in detail now. We will meet them again in the examples below.

Let the domain of definition of the function y = f(x) be the union of several intervals. When finding the range of values of such a function, the sets of values on each interval are determined and their union is taken.

Example.

Find the range of the function.

Solution.

The denominator of our function should not go to zero, that is, .

First, let's find the set of function values on the open ray.

Derivative of a function is negative on this interval, that is, the function decreases on it.

We found that as the argument tends to minus infinity, the function values asymptotically approach unity. When x changes from minus infinity to two, the values of the function decrease from one to minus infinity, that is, on the interval under consideration, the function takes on a set of values. We do not include unity, since the values of the function do not reach it, but only asymptotically tend to it at minus infinity.

We proceed similarly for the open beam.

On this interval the function also decreases.

The set of function values on this interval is the set .

Thus, the desired range of values of the function is the union of the sets and .

Graphic illustration.

Special attention should be paid to periodic functions. The range of values of periodic functions coincides with the set of values on the interval corresponding to the period of this function.

Example.

Find the range of the sine function y = sinx.

Solution.

This function is periodic with a period of two pi. Let's take a segment and define the set of values on it.

The segment contains two extremum points and .

We calculate the values of the function at these points and on the boundaries of the segment, select the smallest and largest value:

Hence, .

Example.

Find the range of a function .

Solution.

We know that the arc cosine range is the segment from zero to pi, that is, or in another post. Function can be obtained from arccosx by shifting and stretching along the abscissa axis. Such transformations do not affect the range of values, therefore, . Function obtained from stretching three times along the Oy axis, that is, . And the last stage of transformation is a shift of four units down along the ordinate. This leads us to double inequality

Thus, the required range of values is .

Let us give the solution to another example, but without explanations (they are not required, since they are completely similar).

Example.

Define Function Range .

Solution.

Let us write the original function in the form . The range of values of the power function is the interval. That is, . Then

Hence, .

To complete the picture, we should talk about finding the range of values of a function that is not continuous on the domain of definition. In this case, we divide the domain of definition into intervals by break points, and find sets of values on each of them. By combining the resulting sets of values, we obtain the range of values of the original function. We recommend remembering 3 on the left, the values of the function tend to minus one, and as x tends to 3 on the right, the values of the function tend to plus infinity.

Thus, we divide the domain of definition of the function into three intervals.

On the interval we have the function . Since then

Thus, the set of values of the original function on the interval is [-6;2] .

On the half-interval we have a constant function y = -1. That is, the set of values of the original function on the interval consists of a single element .

The function is defined for all valid argument values. Let us find out the intervals of increase and decrease of the function.

The derivative vanishes at x=-1 and x=3. Let's mark these points on the number line and determine the signs of the derivative on the resulting intervals.

The function decreases by , increases by [-1; 3] , x=-1 minimum point, x=3 maximum point.

Let's calculate the corresponding minimum and maximum of the function:

Let's check the behavior of the function at infinity:

The second limit was calculated using .

Let's make a schematic drawing.

When the argument changes from minus infinity to -1, the function values decrease from plus infinity to -2e, when the argument changes from -1 to 3, the function values increase from -2e to, when the argument changes from 3 to plus infinity, the function values decrease from to zero, but they don't reach zero.