An open algebra lesson on the topic “The relationship between the sine and cosine of the same angle” (grade 10). Basic trigonometric identities, their formulations and derivation
Let's try to find the relationship between the main trigonometric functions the same angle.
Relationship between cosine and sine of the same angle
The following figure shows the coordinate system Oxy with the part of the unit semicircle ACB depicted in it with the center at point O. This part is the arc of the unit circle. The unit circle is described by the equation
- x 2 +y 2 =1.
As is already known, the ordinate y and abscissa x can be represented as the sine and cosine of the angle using the following formulas:
- sin(a) = y,
- cos(a) = x.
Substituting these values into the equations of the unit circle we have the following equality
- (sin(a)) 2 + (cos(a)) 2 =1,
This equality holds for any value of angle a. It's called the basic trigonometric identity.
From the main trigonometric identity, you can express one function through another.
- sin(a) = ±√(1-(cos(a)) 2),
- cos(a) = ±√(1-(sin(a)) 2).
The sign on the right side of this formula is determined by the sign of the expression on the left side of this formula.
For example.
Calculate sin(a) if cos(a)=-3/5 and pi Let's use the formula given above: Since pi Now, let's try to find the relationship between the tangent and cotangents. By definition, tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a). Let's multiply these equalities and get tg(a)*ctg(a) =1. From this equality one can express one function through another. We get: It should be understood that these equalities are valid only when tg and ctg exist, that is, for any a, except a = k*pi/2, for any integer k. Now let's try, using the basic trigonometric identity, to find the relationship between tangent and cosine. Let's divide the main trigonometric identity by (cos(a)) 2. (cos(a) is not equal to zero, otherwise the tangent would not exist. We obtain the following equality ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2. Dividing term by term we get: As noted above, this formula is correct if cos(a) is not equal to zero, that is, for all angles a, except a=pi/2 +pi*k, for any integer k. Subject: Trigonometric formulas (25 hours)
And now the screen presents self-assessment rubrics on this topic. Mark what level you would like to reach today.
I understood the topic and can solve examples using the algorithm, looking at the notebook, but with the help of leading questions (card - instructions). I understood the topic and can solve examples using the algorithm, looking at the notebook, using the teacher’s instructions. I understood the topic and can solve examples using the algorithm, looking at the notebook, without leading questions or instructions. I understood the topic and can solve examples using the algorithm without looking at the notebook. Whatever level you choose, first carefully review all the tasks that I have given you, and then complete the task corresponding to the level you have chosen (there are tasks in front of you in four options, the number of the option corresponds to the levels of self-esteem.) 1 option
Option 4
Now guys, let's check the answers. The correct answers are displayed on the screen, and students check their work and add points to the lesson card for Tasks No. 4.
Evaluate yourself using the lesson map. Calculate your points and put them on the card. LESSON MAP “DEPENDENCE BETWEEN SINE, COSINE AND TANGENT OF THE SAME ANGLE” Student ________________________________________________________________________________ 1. I know the material from previous lessons Points I answered all the questions correctly without notes. I answered without a note with one mistake. I answered without taking notes and made more than one mistake. I answered all the questions correctly using the notes. I answered using my notes, with one mistake. I answered using my notes and made more than one mistake 2. I have completed recording the examples. Points I completed all tasks without errors I completed with one error I completed the tasks and made more than two mistakes 3. I deduced the formula for finding sine and cosine Points I got the formulas right I derived the formulas and made one mistake I derived the formulas with the help of my teacher 4. I applied my knowledge on the topic: “The relationship between the sine, cosine and tangent of the same angle” when solving independent work Points I solved the examples of option 1 without errors. I solved the examples of option 1 and made a mistake. I solved the examples of option 2 without errors. I solved the examples of option 2 and made a mistake. I solved examples 3 options without errors I solved the examples of option 3 and made a mistake. I solved examples 4 options without errors. I solved the examples of option 4 and made a mistake. 5. Rate yourself: I understood the derivation of the formulas and can solve examples on this topic with a notebook and the help of a teacher. I understood the derivation of the formulas and can solve examples on my own without a notebook, just by looking at the formulas. I understood the derivation of formulas and can solve examples on my own without a notebook; if I forget a formula, I can deduce it myself. My points: __________ Maximum number of points – 22 18 – 22 points - score “5” 15 – 17 points - score “4” 11–14 points - score “3” Less than 11 points - you need to come for a consultation in the coming days, the material has not yet been mastered. Vera Anatolyevna Golovatova, mathematics teacher GB POU "Okhta College" Summary of two lessons for studentsI
course (10th grade) on the topic: “The relationship between sine, cosine and tangent of the same angle” Target: study the relationship between sine, cosine and tangent of the same angle. To achieve this goal it is necessary: Know: formulations of definitions of basic trigonometric functions (sine, cosine and tangent); signs of trigonometric functions by quarters; set of values of trigonometric functions; basic formulas of trigonometry. Understand: that the basic trigonometric identity can only be used for the same argument; algorithm for calculating one trigonometric function through another. Apply: the ability to correctly choose the right formula to solve a specific task; ability to work with simple fractions; ability to perform transformations of trigonometric expressions. Analysis: analyze errors in the logic of reasoning. Synthesis: suggest your own way of solving examples; create a crossword using the knowledge you have gained. Grade: knowledge and skills on this topic for use in other sections of algebra. Equipment:
layout of a trigonometric circle, handouts with formulas and tables of values of trigonometric functions, computer, multimedia projector, presentation, sheets with tasks for independent work. Sources used: Algebra and beginnings of analysis: Textbook for grades 10-11. general education institutions / Sh.A.Alimov, Yu.V. Sidorov et al. Education, 2006. Open Bank assignments for preparing for the Unified State Exam in mathematics, 2011. INTERNET network resources. Brief lesson plan: Organizational moment. Greetings. Communicating the purpose of the lesson and the lesson plan - 3-5 min. Updating knowledge and skills. Students are given lesson cards and given explanations on how to work with them. Questions are displayed on the screen; students write down answers in a notebook; The teacher displays the correct answer on the screen. After completing the survey, students add points to the lesson card for Tasks No. 1
– 10 min. Explanation of new material. The teacher derives the formula for the basic trigonometric identity - 5 min. Students are asked to independently complete the recording of the examples displayed on the screen, check the correctness of the answers and add points to the lesson card for Tasks No. 2 –
5 min. In the notebook, students are asked to independently express sine through cosine and cosine through sine from the basic trigonometric identity. The correct answer is displayed on the screen, students check and add points to the lesson card for Tasks No. 3
– 5-7 min. The teacher solves examples on the blackboard using the basic trigonometric identity. Students answer the teacher’s questions during the explanation and write down examples in their notebooks - 15 min. The teacher derives formulas showing the relationship between tangent and cotangent, students take an active part in deriving formulas, answer questions and make notes in a notebook - 5 min. The teacher derives formulas showing the relationship between tangent and cosine, between sine and cotangent - 5 min. Students are called to the board at will and, with the help of the teacher, solve examples using an algorithm. Everyone else writes down and answers questions as necessary - 10 min. Reinforcing the material learned At the end of the lesson, the correct answers are displayed on the screen, students check their answers and add points to the lesson card for Tasks No. 4
– 20 min. Homework: Students write homework assignments in their notebooks - 3 min. After attending seminars on RNS and teaching a lesson using a technology map, it became obvious to me that the rating system stimulates the maximum possible interest of students in a specific topic. In my case, these are the basic formulas of trigonometry. Trigonometry is very often not perceived by students, not so much because of its complexity, but because of the large number of formulas that you need to be able to work with. It is difficult to expect any incredible successes and results after one lesson conducted using a technology map, but it seems to me that the advantages of the rating system when studying trigonometry and mathematics in general are as follows: it became possible to organize and support both work in the classroom and independent, systematic work of students at home; Attendance and level of discipline in lessons should increase; motivation for educational activities increases; Stressful situations when receiving unsatisfactory grades are reduced; creative attitude towards work is stimulated. The only drawback of RNS (as it seems to me) is a large amount of work for the teacher, but this is work for results. After a single lesson taught using this system, students constantly ask whether we will continue to work this way. It means they were hooked by something. And we need to keep working. INDEPENDENT WORK Whatever level you choose, first carefully review all the tasks that I have given to you, and then complete the task corresponding to the level you have chosen (Before you are tasks of four options, the number of the option corresponds to the levels of self-esteem.) 1 option
Instructions:
Instructions:
Solve this example yourself: Option 2
Hint: To determine the cosine function, use formula (3) from today's lesson. Don't forget to determine the sign that will appear in front of the root. To calculate the values of tangent and cotangent, you can use the definition of these functions or use the formulas that we developed today in class. Note. Group the first and third terms of the expression, take the common factor out of brackets.... Option 3
Option 4
Repetition: 1. In which quarter is the angle in 1 radian and what is it approximately equal to? In the first quarter, 1 rad. 57.3° 2. What word is missing in the definition of the sine function? Sine of the angle
called ………… points of the unit circle. ORDINATE 3. What word is missing in the definition of the cosine function? Cosine of the angle
called …………
points of the unit circle. ABSCISSA 4. Complete the formula:
tg
5. Determine the sign of the product: tg
6. What value can sine take?
or
7. Calculate: y
B(x;y)
R
Y=sin
O
x
x=cos
Complete the recording:
x
y
x
y
x
x
x
y
x
y
x
x
Option 1: Option 3: 2.Option: Option 4: Trigonometric identities- these are equalities that establish a connection between sine, cosine, tangent and cotangent of one angle, which allows you to find any of these functions, provided that any other is known. tg \alpha = \frac(\sin \alpha)(\cos \alpha), \enspace ctg \alpha = \frac(\cos \alpha)(\sin \alpha) tg \alpha \cdot ctg \alpha = 1 This identity says that the sum of the square of the sine of one angle and the square of the cosine of one angle is equal to one, which in practice makes it possible to calculate the sine of one angle when its cosine is known and vice versa. When converting trigonometric expressions, this identity is very often used, which allows you to replace the sum of the squares of the cosine and sine of one angle with one and also perform the replacement operation in the reverse order. tg \alpha = \frac(\sin \alpha)(\cos \alpha),\enspace These identities are formed from the definitions of sine, cosine, tangent and cotangent. After all, if you look at it, then by definition the ordinate y is a sine, and the abscissa x is a cosine. Then the tangent will be equal to the ratio \frac(y)(x)=\frac(\sin \alpha)(\cos \alpha), and the ratio \frac(x)(y)=\frac(\cos \alpha)(\sin \alpha)- will be a cotangent. Let us add that only for such angles \alpha at which the trigonometric functions included in them make sense, the identities will hold, ctg \alpha=\frac(\cos \alpha)(\sin \alpha). For example: tg \alpha = \frac(\sin \alpha)(\cos \alpha) is valid for angles \alpha that are different from \frac(\pi)(2)+\pi z, A ctg \alpha=\frac(\cos \alpha)(\sin \alpha)- for an angle \alpha other than \pi z, z is an integer. tg \alpha \cdot ctg \alpha=1 This identity is valid only for angles \alpha that are different from \frac(\pi)(2) z. Otherwise, either cotangent or tangent will not be determined. Based on the above points, we obtain that tg \alpha = \frac(y)(x), A ctg \alpha=\frac(x)(y). It follows that tg \alpha \cdot ctg \alpha = \frac(y)(x) \cdot \frac(x)(y)=1. Thus, the tangent and cotangent of the same angle at which they make sense are mutually inverse numbers. tg^(2) \alpha + 1=\frac(1)(\cos^(2) \alpha)- the sum of the square of the tangent of the angle \alpha and 1 is equal to the inverse square of the cosine of this angle. This identity is valid for all \alpha other than \frac(\pi)(2)+ \pi z. 1+ctg^(2) \alpha=\frac(1)(\sin^(2)\alpha)- the sum of 1 and the square of the cotangent of the angle \alpha is equal to the inverse square of the sine of the given angle. This identity is valid for any \alpha different from \pi z. Find \sin \alpha and tg \alpha if \cos \alpha=-\frac12 And \frac(\pi)(2)< \alpha < \pi
; Show solution Solution The functions \sin \alpha and \cos \alpha are related by the formula \sin^(2)\alpha + \cos^(2) \alpha = 1. Substituting into this formula \cos \alpha = -\frac12, we get: \sin^(2)\alpha + \left (-\frac12 \right)^2 = 1 This equation has 2 solutions: \sin \alpha = \pm \sqrt(1-\frac14) = \pm \frac(\sqrt 3)(2) By condition \frac(\pi)(2)< \alpha < \pi
. In the second quarter the sine is positive, so \sin \alpha = \frac(\sqrt 3)(2). In order to find tan \alpha, we use the formula tg \alpha = \frac(\sin \alpha)(\cos \alpha) tg \alpha = \frac(\sqrt 3)(2) : \frac12 = \sqrt 3 Find \cos \alpha and ctg \alpha if and \frac(\pi)(2)< \alpha < \pi
. Show solution Solution Substituting into the formula \sin^(2)\alpha + \cos^(2) \alpha = 1 given number \sin \alpha=\frac(\sqrt3)(2), we get \left (\frac(\sqrt3)(2)\right)^(2) + \cos^(2) \alpha = 1. This equation has two solutions \cos \alpha = \pm \sqrt(1-\frac34)=\pm\sqrt\frac14. By condition \frac(\pi)(2)< \alpha < \pi
. In the second quarter the cosine is negative, so \cos \alpha = -\sqrt\frac14=-\frac12. In order to find ctg \alpha , we use the formula ctg \alpha = \frac(\cos \alpha)(\sin \alpha). We know the corresponding values. ctg \alpha = -\frac12: \frac(\sqrt3)(2) = -\frac(1)(\sqrt 3). In this article we will take a comprehensive look. Basic trigonometric identities are equalities that establish a connection between the sine, cosine, tangent and cotangent of one angle, and allow one to find any of these trigonometric functions through a known other. Let us immediately list the main trigonometric identities that we will analyze in this article. Let's write them down in a table, and below we'll give the output of these formulas and provide the necessary explanations. Page navigation. Sometimes they do not talk about the main trigonometric identities listed in the table above, but about one single basic trigonometric identity type That is, it is the equality that is of particular interest, which was given the name of the main trigonometric identity. Before proving the main trigonometric identity, we give its formulation: the sum of the squares of the sine and cosine of one angle is identically equal to one. Now let's prove it. The basic trigonometric identity is very often used when converting trigonometric expressions. It allows the sum of the squares of the sine and cosine of one angle to be replaced by one. No less often, the basic trigonometric identity is used in the reverse order: unit is replaced by the sum of the squares of the sine and cosine of any angle. Identities connecting tangent and cotangent with sine and cosine of one angle of view and Thanks to such obviousness of the identities and In conclusion of this paragraph, it should be noted that the identities and An even more obvious trigonometric identity than the previous two is the identity connecting the tangent and cotangent of one angle of the form Proof of the formula So, the tangent and cotangent of the same angle at which they make sense are .Relationship between tangent and cotangent of the same angle
Lesson 6 – 7: The relationship between sine, cosine and tangent of the same angle.
Target: study the relationship between sine, cosine and tangent of the same angle. To achieve this goal it is necessary:Know:
formulations of definitions of basic trigonometric functions (sine, cosine and tangent); signs of trigonometric functions by quarters; set of values of trigonometric functions; basic formulas of trigonometry.
Understand:
that the basic trigonometric identity can only be used for the same argument; algorithm for calculating one trigonometric function through another.
Apply:
the ability to correctly choose the right formula to solve a specific task; ability to work with simple fractions; ability to perform transformations of trigonometric expressions.
Analysis:
analyze errors in the logic of reasoning.
Synthesis:
suggest your own way of solving examples; create a crossword using the knowledge you have gained.
Grade:
Equipment:
layout of a trigonometric circle, handouts with formulas and tables of values of trigonometric functions, computer, multimedia projector, presentation, sheets with tasks for independent work. Lesson progress: knowledge and skills on this topic for use in other sections of algebra.
Organizational moment.
Greetings. Communicating the purpose of the lesson and the lesson plan. Updating knowledge and skills.
Students are given lesson cards and given explanations on how to work with them. Questions are displayed on the screen; students write down answers in a notebook; The teacher displays the correct answer on the screen. After completing the survey, students add points to the lesson card for Tasks No. 1.
In which quarter is an angle of 1 radian located and what is it approximately equal to?
(In the first quarter, 1 rad 57.3 0). What word is missing from the definition of the sine function?
The sine of angle is the ............ points of the unit circle. (Ordinate) What word is missing in the definition of the cosine function?
Cosine of the angle
called ............ points of the unit circle (abscissa). What values can sine take?
 ()
() Explanation of new material.
AND  Let us depict a unit circle with the center at point O. Let us assume that by rotating the radius OA, equal to R, by an angle , the radius OB is obtained (Fig. 5). Then by definition
Let us depict a unit circle with the center at point O. Let us assume that by rotating the radius OA, equal to R, by an angle , the radius OB is obtained (Fig. 5). Then by definition 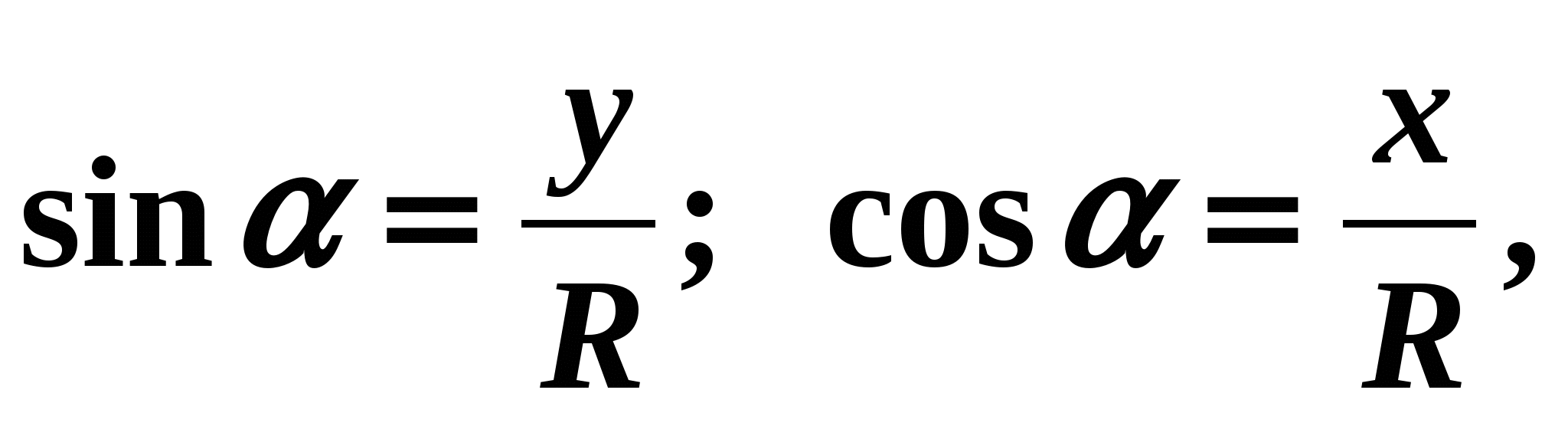 Where
Where  – abscissa of point B,
– abscissa of point B, 
 – its ordinate. It follows that Point B belongs to the circle. Therefore, its coordinates satisfy the equation
– its ordinate. It follows that Point B belongs to the circle. Therefore, its coordinates satisfy the equation  Taking advantage of what we get
Taking advantage of what we get  (1).
We have obtained an equality that is valid for any values of the letters included in it. What are such equalities called? That's right - identities. Equality (1) is called basic trigonometric identity. In equality (1) can take any value. Complete the recording yourself:
(1).
We have obtained an equality that is valid for any values of the letters included in it. What are such equalities called? That's right - identities. Equality (1) is called basic trigonometric identity. In equality (1) can take any value. Complete the recording yourself:
1.
Please check that your entry is correct. Add points to your lesson card for Tasks No. 2.
Let's continue. We have derived the main trigonometric identity, but why do we need it? That's right - to find the cosine value from one known sine value and vice versa. Now you and I can always use the basic trigonometric identity, but the main thing is for the same argument. In the notebook, students are asked to independently express sine through cosine and cosine through sine from the basic trigonometric identity. Two students are called to the board to check. One is asked to express the sine through the cosine, the second - the cosine through the sine. The correct answer is displayed on the screen: 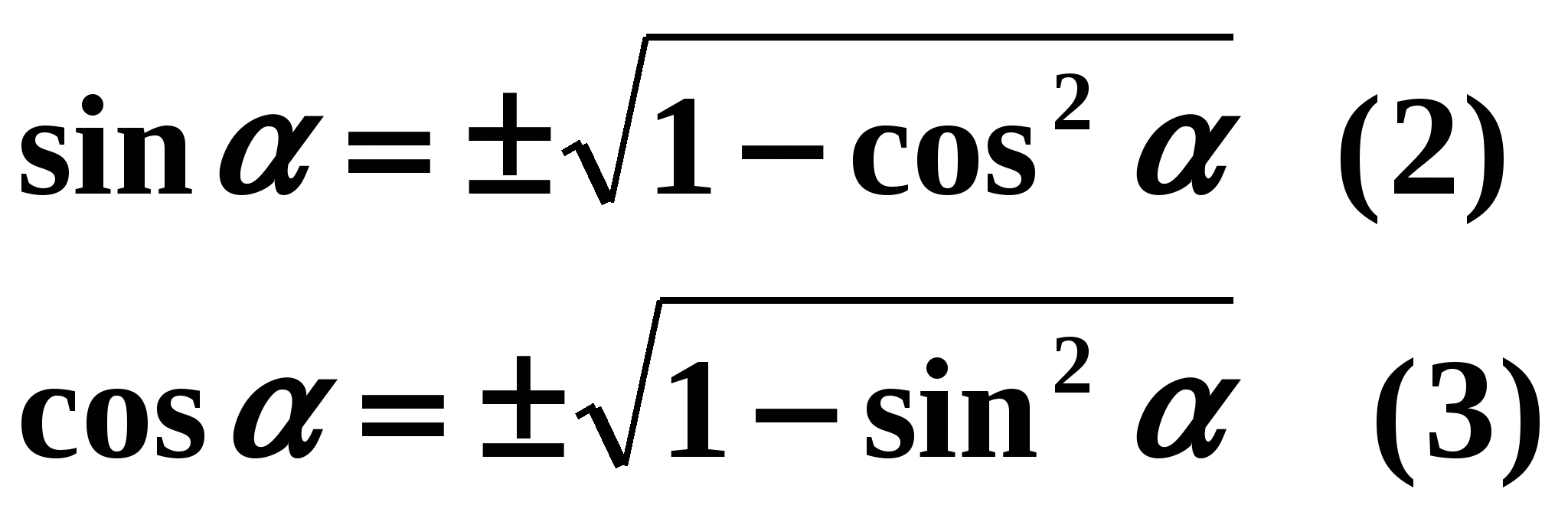 Students check their answers and add points to the lesson card for Tasks No. 3.
In these formulas, what does the sign in front of the root depend on? (It depends on which quadrant the angle of the trigonometric function we are defining is located in).
Students check their answers and add points to the lesson card for Tasks No. 3.
In these formulas, what does the sign in front of the root depend on? (It depends on which quadrant the angle of the trigonometric function we are defining is located in).
Example 1
. Calculate  If
If 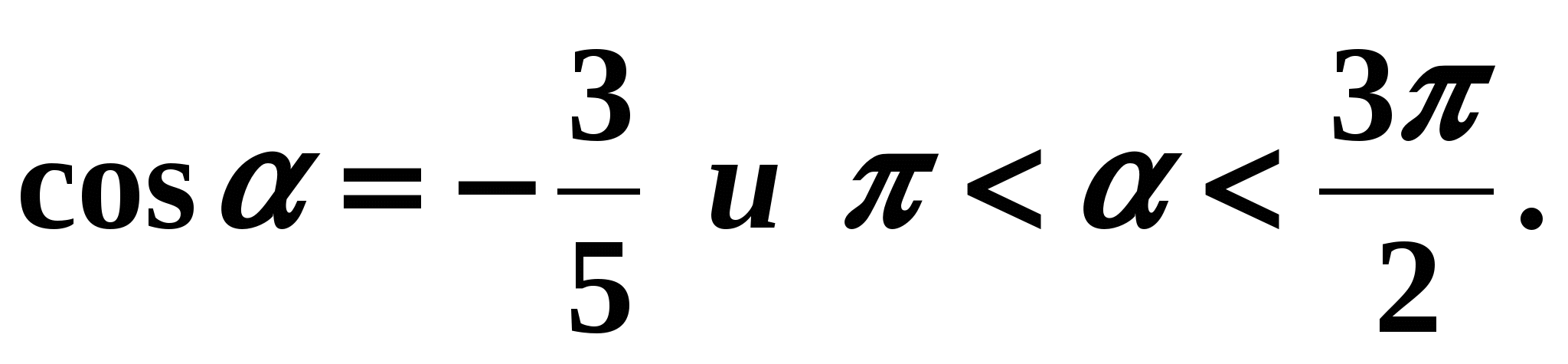 Determine the quarter in which the angle is located
Determine the quarter in which the angle is located  . Quarter – III. Let us remember that the sine in the third quarter is negative, i.e. in formula (2) you need to put the “-” sign in front of the root: Example 2.
Calculate
. Quarter – III. Let us remember that the sine in the third quarter is negative, i.e. in formula (2) you need to put the “-” sign in front of the root: Example 2.
Calculate 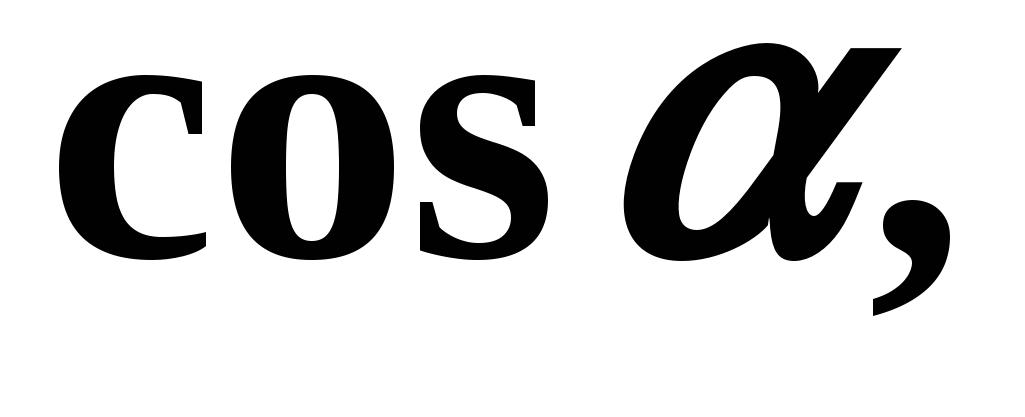 If
If  We determine the quarter in which the angle is located. Quarter – IV, cosine in the fourth quarter is positive. Therefore, in formula (3) the “+” sign is needed before the root:
We determine the quarter in which the angle is located. Quarter – IV, cosine in the fourth quarter is positive. Therefore, in formula (3) the “+” sign is needed before the root:
Let's find out now relationship between tangent and cotangent. By definition of tangent and cotangent 
Multiplying these equalities, we get: 
From equality (4) we can express  through
through  and vice versa:
and vice versa: 
Equalities (4) – (6) are true for all values for which  make sense, i.e. when
make sense, i.e. when  Let us now derive formulas expressing the relationship between tangent and cosine, as well as cotangent and sine of the same argument. Dividing both sides of equality (1) by
Let us now derive formulas expressing the relationship between tangent and cosine, as well as cotangent and sine of the same argument. Dividing both sides of equality (1) by  , we get:
, we get: 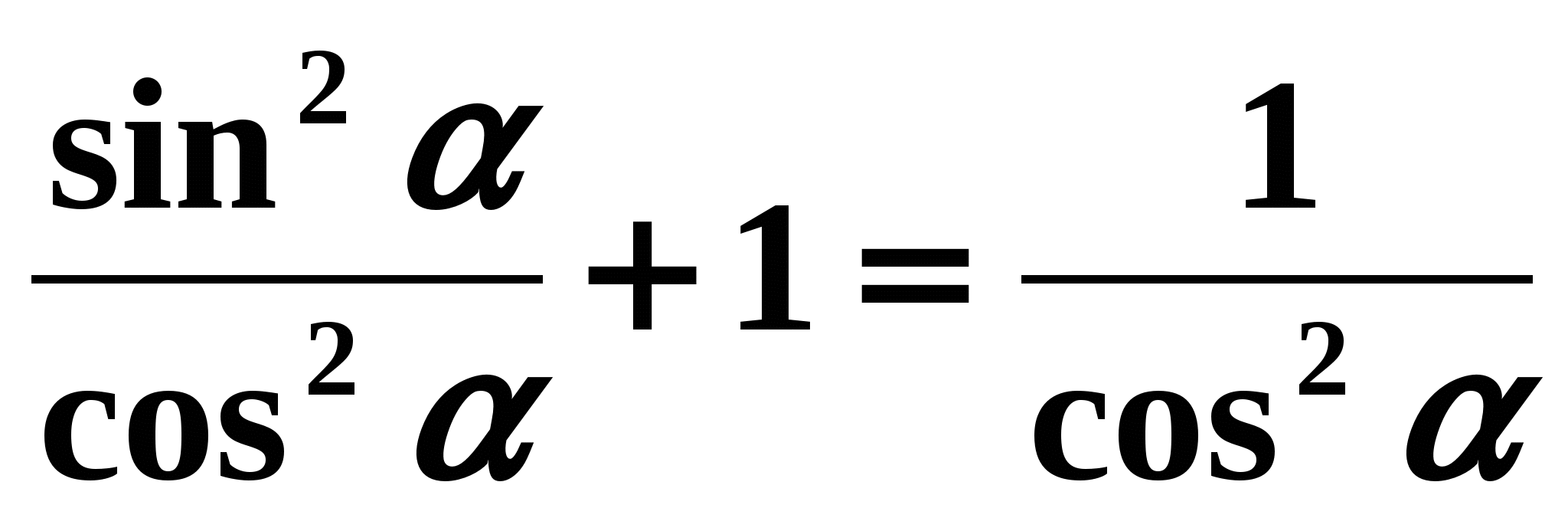 those.
those. 
If both sides of equality (1) are divided by  , then we will have:
, then we will have:  those.
those. 
Let's look at examples of using the derived formulas to find the values of trigonometric functions from a known value of one of them.
Example 1.
Let's find if it is known that 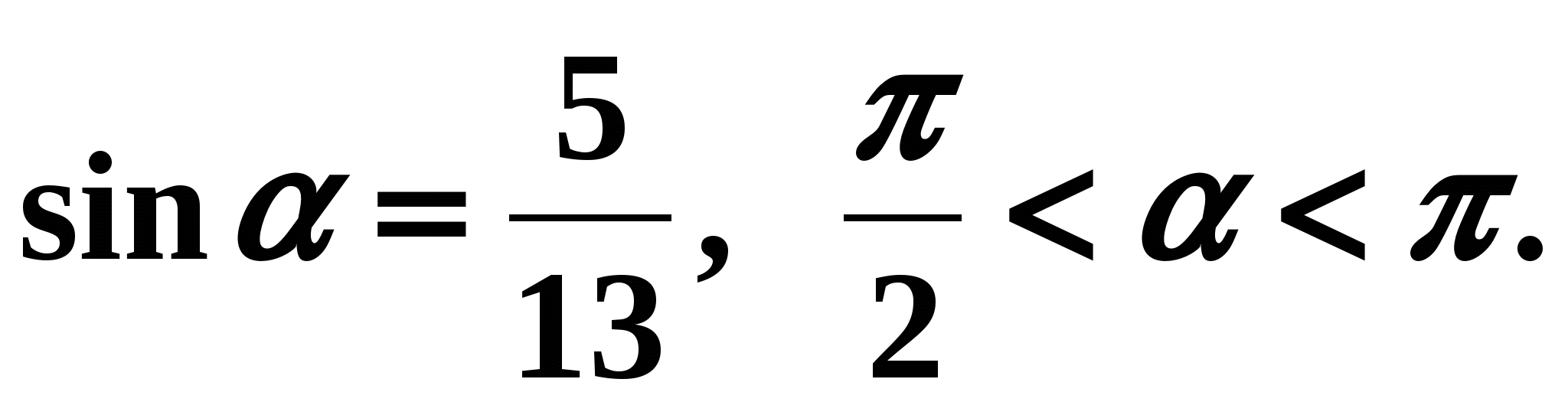 Solution:
Solution: 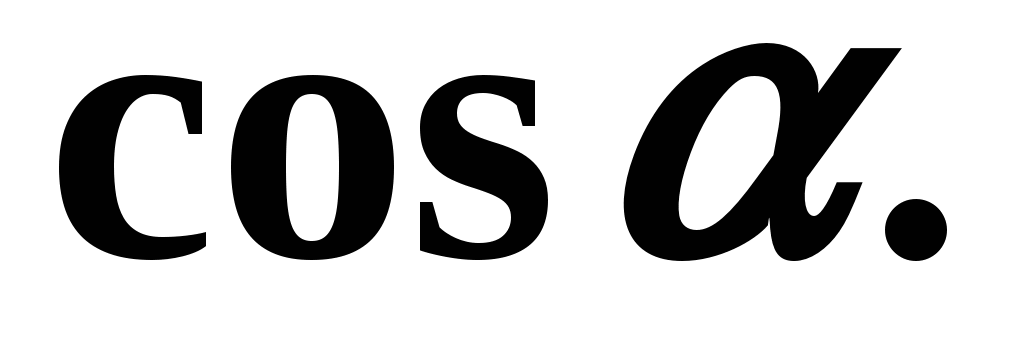
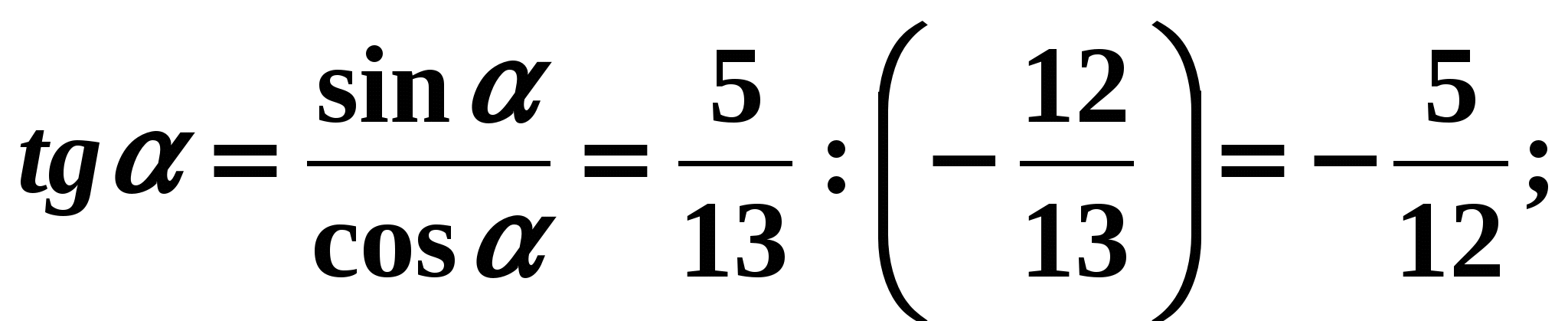
To find the cotangent of angle it is convenient to use formula (6):
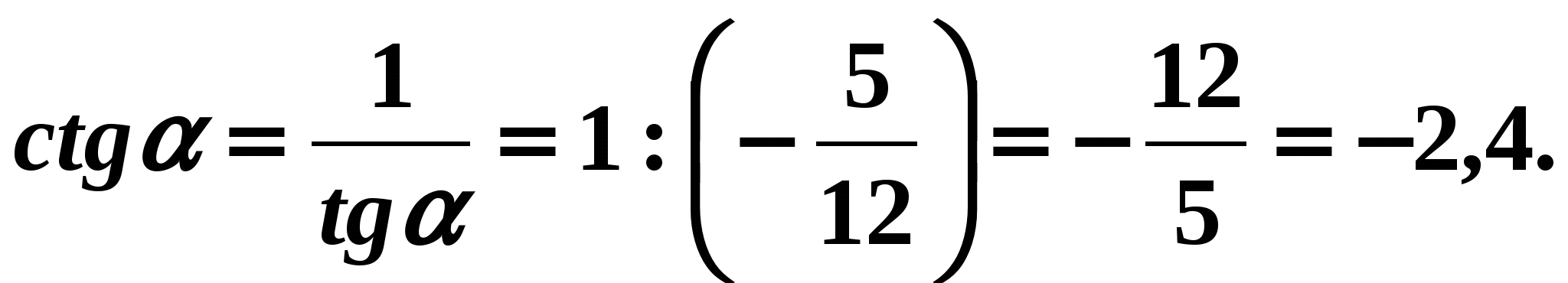 Answer:
Answer:
Example 2.
It is known that  . Let's find all the other trigonometric functions. Solution:
. Let's find all the other trigonometric functions. Solution: Let's use the formula (7).
We have:
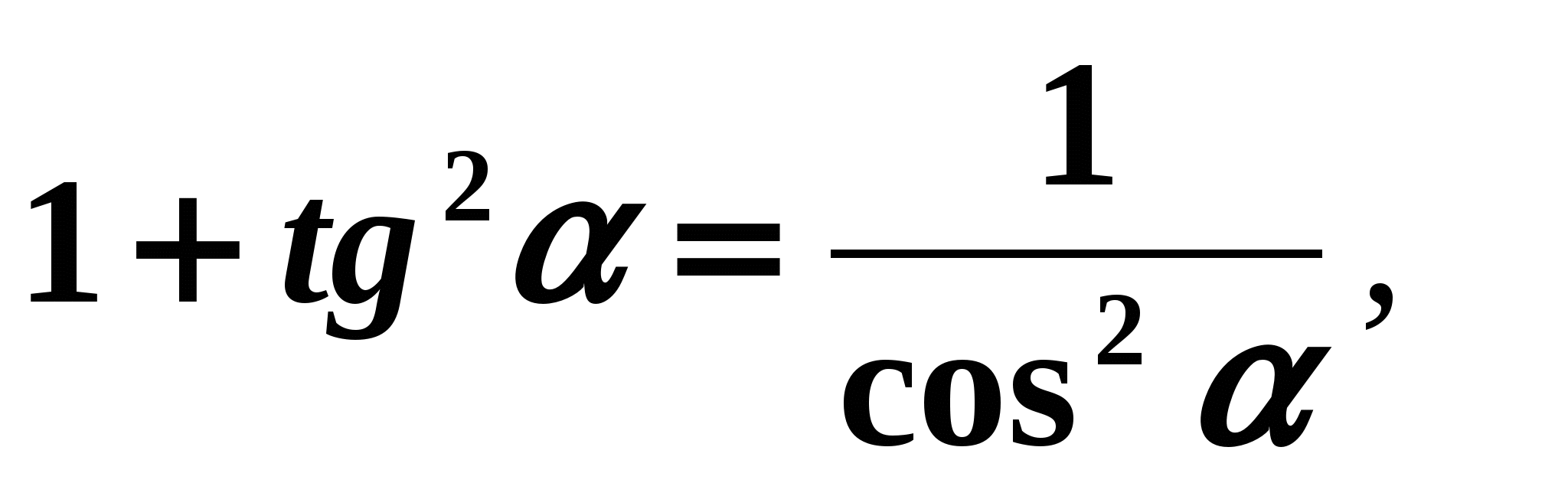
 ,
,  . According to the conditions of the problem, angle is the angle of 1 quarter, so its cosine is positive. Means
. According to the conditions of the problem, angle is the angle of 1 quarter, so its cosine is positive. Means 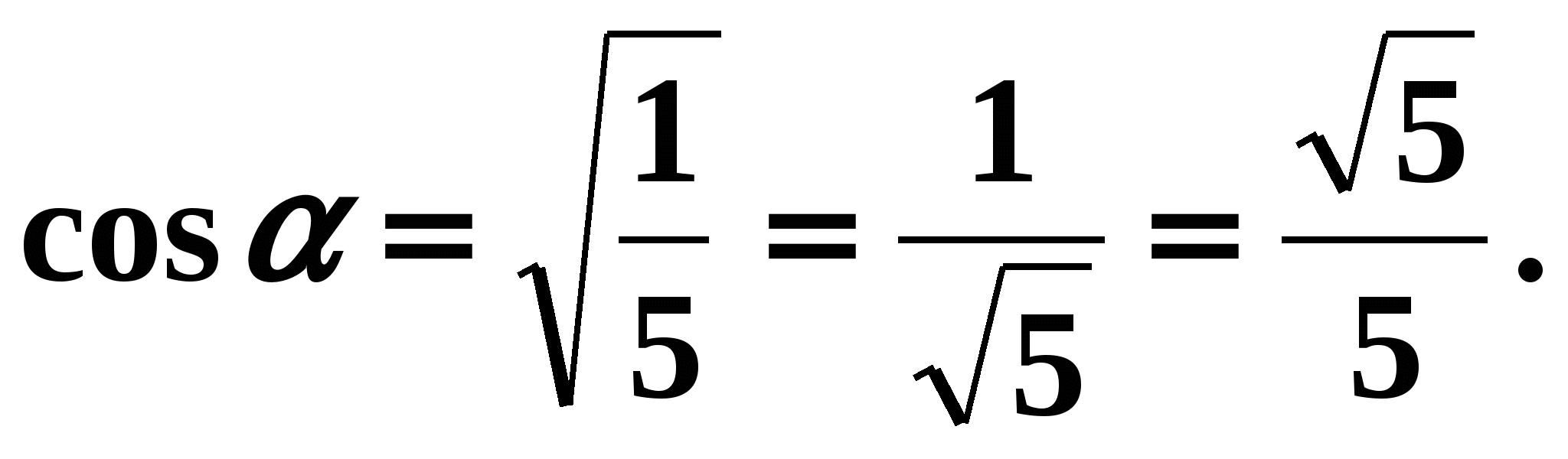

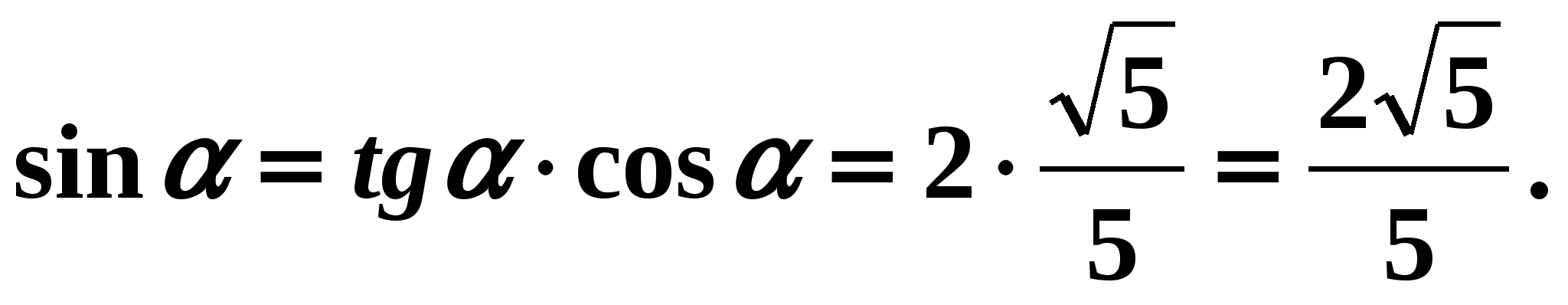
Answer: 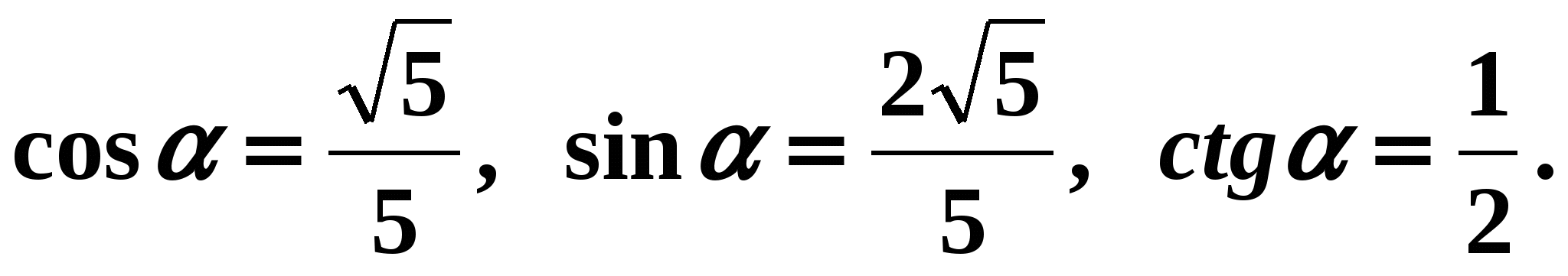 Established relationships between trigonometric functions of the same argument make it possible to simplify trigonometric expressions.
Established relationships between trigonometric functions of the same argument make it possible to simplify trigonometric expressions.
Example 3.
Let's simplify the expression: 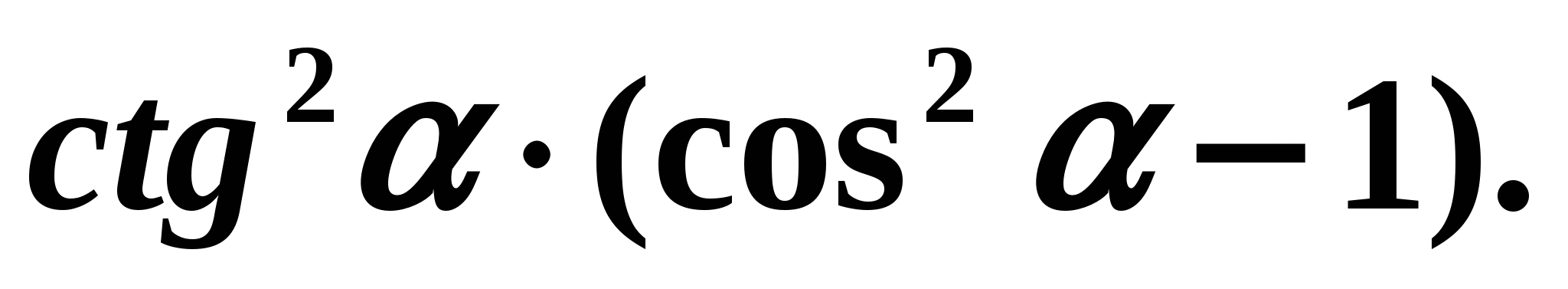 Solution: Let's use the formulas:
Solution: Let's use the formulas: 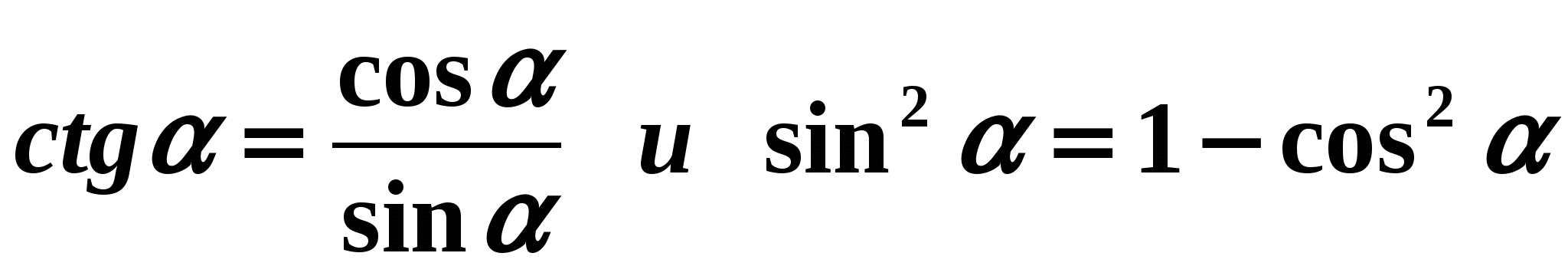 . We get:
. We get: Consolidation.
 Instructions:
Instructions:
Homework.
6
Write down all the derived formulas in the reference book. According to textbook No. 459 (3, 5), No. 460 (1)
"Brief Plan"View document contents
"Reflection"View document contents
"Independent work"





View presentation content
"Presentation"















Finding tangent and cotangent using sine and cosine
Relationship between tangent and cotangent
Relationships between tangent and cosine, cotangent and sine
Examples with solutions to problems using trigonometric identities
Example 1
Example 2
Relationship between sine and cosine of one angle
![]() . The explanation for this fact is quite simple: the equalities are obtained from the main trigonometric identity after dividing both of its parts by and respectively, and the equalities
. The explanation for this fact is quite simple: the equalities are obtained from the main trigonometric identity after dividing both of its parts by and respectively, and the equalities  And
And ![]() follow from the definitions of sine, cosine, tangent and cotangent. We'll talk about this in more detail in the following paragraphs.
follow from the definitions of sine, cosine, tangent and cotangent. We'll talk about this in more detail in the following paragraphs.Tangent and cotangent through sine and cosine
![]() follow immediately from the definitions of sine, cosine, tangent and cotangent. Indeed, by definition, sine is the ordinate of y, cosine is the abscissa of x, tangent is the ratio of the ordinate to the abscissa, that is,
follow immediately from the definitions of sine, cosine, tangent and cotangent. Indeed, by definition, sine is the ordinate of y, cosine is the abscissa of x, tangent is the ratio of the ordinate to the abscissa, that is, ![]() , and the cotangent is the ratio of the abscissa to the ordinate, that is,
, and the cotangent is the ratio of the abscissa to the ordinate, that is, ![]() .
.![]() Tangent and cotangent are often defined not through the ratio of abscissa and ordinate, but through the ratio of sine and cosine. So the tangent of an angle is the ratio of the sine to the cosine of this angle, and the cotangent is the ratio of the cosine to the sine.
Tangent and cotangent are often defined not through the ratio of abscissa and ordinate, but through the ratio of sine and cosine. So the tangent of an angle is the ratio of the sine to the cosine of this angle, and the cotangent is the ratio of the cosine to the sine.![]() take place for all angles at which the trigonometric functions included in them make sense. So the formula is valid for any , other than (otherwise the denominator will have zero, and we did not define division by zero), and the formula
take place for all angles at which the trigonometric functions included in them make sense. So the formula is valid for any , other than (otherwise the denominator will have zero, and we did not define division by zero), and the formula ![]() - for all , different from , where z is any .
- for all , different from , where z is any .Relationship between tangent and cotangent
![]() . It is clear that it holds for any angles other than , otherwise either the tangent or the cotangent are not defined.
. It is clear that it holds for any angles other than , otherwise either the tangent or the cotangent are not defined.![]() very simple. By definition and from where
very simple. By definition and from where  . The proof could have been carried out a little differently. Since
. The proof could have been carried out a little differently. Since ![]() , That
, That  .
.









