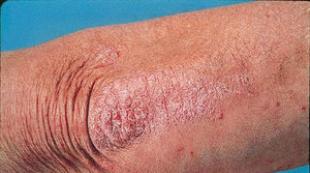
Нахождение области значений функции по ее графику. Область определения функции

Функция-это модель. Определим X, как множество значений независимой переменной // независимая -значит любая.

Функция это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого х есть один у.

Из определения следует, что существует два понятия- независимая переменная (которую обозначаем х и она может принимать любые значения) и зависимая переменная (которую обозначаем y или f(х) и она высчитывается из функции, когда мы подставляем х).

НАПРИМЕР у=5+х

1. Независимая -это х, значит берем любое значение, пусть х=3

2. а теперь вычисляем у, значит у=5+х=5+3=8. (у зависима от х, потому что какой х подставим, такой у и получим)

Говорят, что переменная y функционально зависит от переменной x и обозначается это следующим образом: y = f (x).

НАПРИМЕР.

1.у=1/х. (наз.гипербола)

2. у=х^2. (наз. парабола)

3.у=3х+7. (наз. прямая)

4. у= √ х. (наз. ветвь параболы)

Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.

Область определения функции

Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).

Рассмотрим D (у) для 1.,2.,3.,4.

1. D (у)= (∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.

2. D (у)= (∞; +∞)//всё мн-во действит.чисел

3. D (у)= (∞; +∞)//всё мн-во действит.чисел

4. D (у)= .

Наконец, если задана комбинация различных функций, то область определения представляет собой пересечение областей определения всех этих функций. Например, y=sin(2*x)+x/√(x+2)+arcsin(x−6)+lg(x−6). Сначала найдите область определения всех слагаемых. Sin(2*x) определен на всей числовой прямой. Для функции x/√(x+2) решите неравенство x+2>0 и область определения будет (-2; +∞). Область определения функции arcsin(x−6) задается двойным неравенством -1≤x-6≤1, то есть получается отрезок . Для логарифма имеет место неравенство x−6>0, а это есть интервал (6; +∞). Таким образом, областью определения функции будет множество (-∞; +∞)∩(-2; +∞)∩∩(6; +∞), то есть (6; 7].

Видео по теме

Источники:

• область определения функции с логарифмом

Функция - это понятие, отражающее связь между элементами множеств или другими словами это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

В математике имеется достаточно небольшое количество элементарных функций, область определения которых ограничена. Все остальные "сложные" функции - это всего лишь их сочетания и комбинации.

1. Дробная функция - ограничение на знаменатель.

2. Корень четной степени - ограничение на подкоренное выражение.

3. Логарифмы - ограничение на основание логарифма и подлогарифмическое выражение.

3. Тригонометрические tg(x) и ctg(x) - ограничение на аргумент.

Для тангенса:

4. Обратные тригонометрические функции.

Арксинус	Арккосинус	Арктангенс, Арккотангенс

Далее решаются следующие примеры на тему "Область определения функций".

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Пример 6

Пример 7

Пример 8

Пример 9

Пример 10

Пример 11

Пример 12

Пример 13

Пример 14

Пример 15

Пример 16

Пример нахождения области определения функции №1

Нахождение области определения любой линейной функции, т.е. функции первой степени:

y = 2x + 3 - уравнение задает прямую на плоскости.

Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?

Попробуем подставить значение х=0

Так как y = 2·0 + 3 = 3 - получили числовое значение, следовательно функция существует при взятом значении переменной х=0.

Попробуем подставить значение х=10

так как y = 2·10 + 3 = 23 - функция существует при взятом значении переменной х=10 .

Попробуем подставить значение х=-10

так как y = 2·(-10) + 3 = -17 - функция существует при взятом значении переменной х=-10 .

Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.

Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.

Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R

Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)

Сделаем вывод:

Для любой функции вида y = ax + b областью определения является множество действительных чисел.

Пример нахождения области определения функции №2

Задана функция вида:

y = 10/(x + 5) - уравнение гиперболы

Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не

обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.

При х = 0 имеем y = 10/(0 + 5) = 2 - функция существует.

При х = 10 имеем y = 10/(10 + 5) = 10/15 = 2/ 3 - функция существует.

При х = -5 имеем y = 10/(-5 + 5) = 10/0 - функция в этой точке не существует.

Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.

В нашем случае:

x + 5 = 0 → x = -5 - в этой точке заданная функция не существует.

x + 5 ≠ 0 → x ≠ -5

Для наглядности изобразим графически:

На графике также видим, что гипербола максимально близко приближается к прямой х = -5 , но самого значения -5 не достигает.

Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5

Формы записи ответа: D(f)=R\{-5} илиD(f)=(-∞;-5) ∪ (-5;+∞) или x∈ R\{-5} илиx∈ (-∞;-5) ∪ (-5;+∞)

Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.

Пример нахождения области определения функции №3

Рассмотрим пример нахождения области определения функции с корнем четной степени:

Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем - неотрицательна.

2х - 8 ≥ 0

Решим простое неравенство:

2х - 8 ≥ 0 → 2х ≥ 8 → х ≥ 4

Заданная функция существует только при найденных значениях х ≥ 4 или D(f)= . Остается найти пересечение множеств таких значений x , что x∈D(f 2) и f 2 (x)∈D(f 1) :

Чтобы arcsinx>0 вспомним свойства функции арксинус . Арксинус возрастает на всей области определения [−1, 1] и обращается в ноль при x=0 , следовательно, arcsinx>0 для любого x из промежутка (0, 1] .

Вернемся к системе:

Таким образом, искомая область определения функции есть полуинтервал (0, 1] .

Ответ:

(0, 1] .

Теперь давайте перейдем к сложным функциям общего вида y=f 1 (f 2 (…f n (x)))) . Область определения функции f в этом случае находится как .

Пример.

Найти область определения функции .

Решение.

Заданную сложную функцию можно расписать как y=f 1 (f 2 (f 3 (x))) , где f 1 – sin , f 2 – функция корень четвертой степени, f 3 – lg .

Нам известно, что D(f 1)=(−∞, +∞) , D(f 2)=}